
Question Number 46330 by Saorey last updated on 24/Oct/18
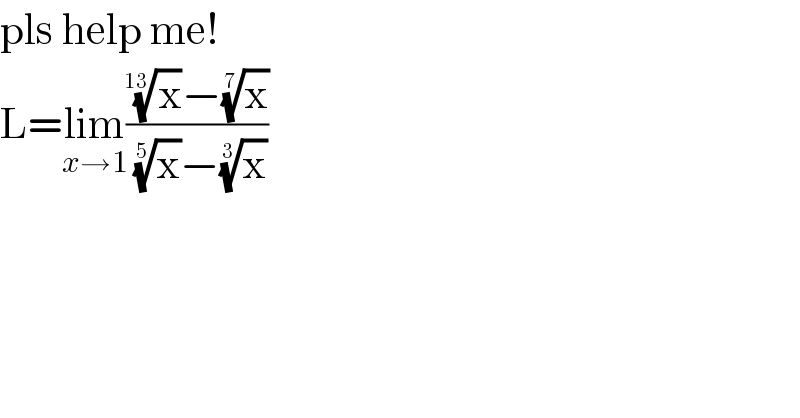
$$\mathrm{pls}\:\mathrm{help}\:\mathrm{me}! \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{13}}]{\mathrm{x}}−\sqrt[{\mathrm{7}}]{\mathrm{x}}}{\sqrt[{\mathrm{5}}]{\mathrm{x}}−\sqrt[{\mathrm{3}}]{\mathrm{x}}} \\ $$
Commented by MJS last updated on 24/Oct/18
![I would again recommend l′Hopital lim_(x→1) ((x^a −x^b )/(x^c −x^d ))=lim_(x→1) (((d/dx)[x^a −x^b ])/((d/dx)[x^c −x^d ]))=lim_(x→1) ((ax^(a−1) −bx^(b−1) )/(cx^(c−1) −dx^(d−1) ))= =lim_(x→1) ((ax^a −bx^b )/(cx^c −dx^d ))=((a−b)/(c−d)) with a=(1/(13)); b=(1/7); c=(1/5); d=(1/3) L=((a−b)/(c−d))=(((1/(13))−(1/7))/((1/5)−(1/3)))=((−(6/(91)))/(−(2/(15))))=((45)/(91))](Q46333.png)
$$\mathrm{I}\:\mathrm{would}\:\mathrm{again}\:\mathrm{recommend}\:\mathrm{l}'\mathrm{Hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{{a}} −{x}^{{b}} }{{x}^{{c}} −{x}^{{d}} }=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left[{x}^{{a}} −{x}^{{b}} \right]}{\frac{{d}}{{dx}}\left[{x}^{{c}} −{x}^{{d}} \right]}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{ax}^{{a}−\mathrm{1}} −{bx}^{{b}−\mathrm{1}} }{{cx}^{{c}−\mathrm{1}} −{dx}^{{d}−\mathrm{1}} }= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{ax}^{{a}} −{bx}^{{b}} }{{cx}^{{c}} −{dx}^{{d}} }=\frac{{a}−{b}}{{c}−{d}} \\ $$$$\mathrm{with}\:{a}=\frac{\mathrm{1}}{\mathrm{13}};\:{b}=\frac{\mathrm{1}}{\mathrm{7}};\:{c}=\frac{\mathrm{1}}{\mathrm{5}};\:{d}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${L}=\frac{{a}−{b}}{{c}−{d}}=\frac{\frac{\mathrm{1}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{7}}}{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}}}=\frac{−\frac{\mathrm{6}}{\mathrm{91}}}{−\frac{\mathrm{2}}{\mathrm{15}}}=\frac{\mathrm{45}}{\mathrm{91}} \\ $$
Commented by hassentimol last updated on 24/Oct/18
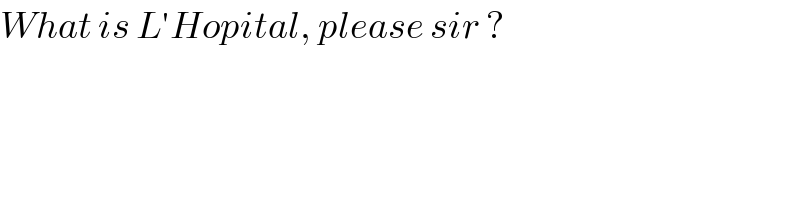
$${What}\:{is}\:{L}'{Hopital},\:{please}\:{sir}\:? \\ $$$$ \\ $$
Commented by MJS last updated on 24/Oct/18
![lim_(x→a) ((f(x))/(g(x)))=lim_(x→a) ((f′(x))/(g′(x))) if f(a)=0 and g(a)=0 xor f(a)=±∞ and g(a)=±∞ example lim_(x→0) (xln x) =lim_(x→0) ((ln x)/x^(−1) ) =lim_(x→0) (((d/dx)[ln x])/((d/dx)[x^(−1) ]))= =lim_(x→0) (x^(−1) /(−x^(−2) )) =lim_(x→0) −x =0](Q46376.png)
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)}\:\mathrm{if}\:{f}\left({a}\right)=\mathrm{0}\:\mathrm{and}\:{g}\left({a}\right)=\mathrm{0}\:\mathrm{xor} \\ $$$${f}\left({a}\right)=\pm\infty\:\mathrm{and}\:{g}\left({a}\right)=\pm\infty \\ $$$$\mathrm{example} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left({x}\mathrm{ln}\:{x}\right)\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:{x}}{{x}^{−\mathrm{1}} }\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left[\mathrm{ln}\:{x}\right]}{\frac{{d}}{{dx}}\left[{x}^{−\mathrm{1}} \right]}= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{−\mathrm{1}} }{−{x}^{−\mathrm{2}} }\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:−{x}\:=\mathrm{0} \\ $$
Answered by ajfour last updated on 24/Oct/18
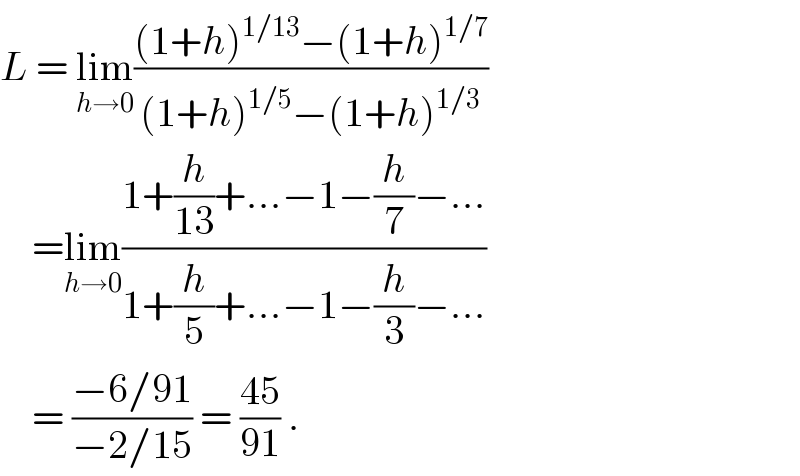
$${L}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+{h}\right)^{\mathrm{1}/\mathrm{13}} −\left(\mathrm{1}+{h}\right)^{\mathrm{1}/\mathrm{7}} }{\left(\mathrm{1}+{h}\right)^{\mathrm{1}/\mathrm{5}} −\left(\mathrm{1}+{h}\right)^{\mathrm{1}/\mathrm{3}} } \\ $$$$\:\:\:\:=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\frac{{h}}{\mathrm{13}}+...−\mathrm{1}−\frac{{h}}{\mathrm{7}}−...}{\mathrm{1}+\frac{{h}}{\mathrm{5}}+...−\mathrm{1}−\frac{{h}}{\mathrm{3}}−...} \\ $$$$\:\:\:\:=\:\frac{−\mathrm{6}/\mathrm{91}}{−\mathrm{2}/\mathrm{15}}\:=\:\frac{\mathrm{45}}{\mathrm{91}}\:. \\ $$
