Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 193175 by Humble last updated on 06/Jun/23

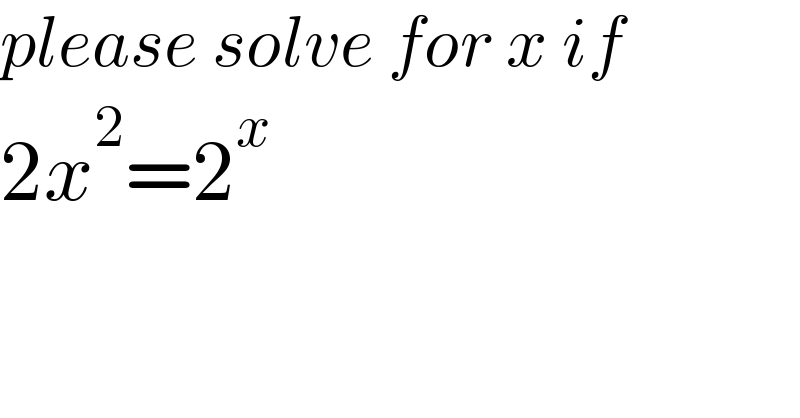
please solve for x if 2x^2 =2^x

$${please}\:{solve}\:{for}\:{x}\:{if} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$

Answered by Frix last updated on 06/Jun/23

Obviously x=1

$$\mathrm{Obviously}\:{x}=\mathrm{1} \\ $$

Answered by Frix last updated on 06/Jun/23

2x^2 =2^x Let x=±(1/( (√2)e^t )) ⇔ t=−(ln (±x)+((ln 2)/2)) e^(−2t) =2^(±(1/( (√2)e^t ))) −2t=±((ln 2)/( (√2)e^t )) te^t =∓((ln 2)/(2(√2))) t=W(∓((ln 2)/(2(√2)))) t≈ { ((.200534631257)),((−2.19024886644∨−.34657359028)) :} ⇒ x= { ((≈−.578620636081)),((≈6.31972235584∨1)) :}

$$\mathrm{2}{x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$$\mathrm{Let}\:{x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{e}^{{t}} }\:\Leftrightarrow\:{t}=−\left(\mathrm{ln}\:\left(\pm{x}\right)+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\mathrm{e}^{−\mathrm{2}{t}} =\mathrm{2}^{\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{e}^{{t}} }} \\ $$$$−\mathrm{2}{t}=\pm\frac{\mathrm{ln}\:\mathrm{2}}{\:\sqrt{\mathrm{2}}\mathrm{e}^{{t}} } \\ $$$${t}\mathrm{e}^{{t}} =\mp\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${t}={W}\left(\mp\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\right) \\ $$$${t}\approx\begin{cases}{.\mathrm{200534631257}}\\{−\mathrm{2}.\mathrm{19024886644}\vee−.\mathrm{34657359028}}\end{cases} \\ $$$$\Rightarrow \\ $$$${x}=\begin{cases}{\approx−.\mathrm{578620636081}}\\{\approx\mathrm{6}.\mathrm{31972235584}\vee\mathrm{1}}\end{cases} \\ $$

Answered by aba last updated on 06/Jun/23

x=1 is solution 2x^2 −2^x =0 ⇒ ((√2)x)^2 −(((√2))^x )^2 =0 ⇒ ((√2)x−((√2))^x )((√2)x+((√2))^x )=0 ⇒(√2)x−((√2))^x =0 ∨ (√2)x+((√2))^x =0 ⇒x.((√2))^(−x) =(1/( (√2))) ∨ x.((√2))^(−x) =−(1/( (√2))) ⇒−xln((√2)).e^(−xln((√2))) =−(((√2)ln((√2)))/2) ∨ −xln((√2)).e^(−xln((√2))) =(((√2)ln((√2)))/2) ⇒−xln((√2))=W(−(((√2)ln((√2)))/2))∨−xln((√2))=W((((√2)ln((√2)))/2)) ⇒x=−(2/(ln(2)))W(−(((√2)ln(2))/4))∨x=−(2/(ln(2)))W((((√2)ln(2))/4)) ⇒x=−(2/(ln(2)))W(−((ln(2))/(2(√2))))≈6.31972 ∨ x=−(2/(ln(2)))W(((ln(2))/(2(√2))))≈−0.578621

$$\mathrm{x}=\mathrm{1}\:\mathrm{is}\:\mathrm{solution} \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} =\mathrm{0}\:\Rightarrow\:\left(\sqrt{\mathrm{2}}\mathrm{x}\right)^{\mathrm{2}} −\left(\left(\sqrt{\mathrm{2}}\right)^{\mathrm{x}} \right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:\left(\sqrt{\mathrm{2}}\mathrm{x}−\left(\sqrt{\mathrm{2}}\right)^{\mathrm{x}} \right)\left(\sqrt{\mathrm{2}}\mathrm{x}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{x}} \right)=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}\mathrm{x}−\left(\sqrt{\mathrm{2}}\right)^{\mathrm{x}} =\mathrm{0}\:\vee\:\sqrt{\mathrm{2}}\mathrm{x}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{x}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}.\left(\sqrt{\mathrm{2}}\right)^{−\mathrm{x}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\vee\:\mathrm{x}.\left(\sqrt{\mathrm{2}}\right)^{−\mathrm{x}} =−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow−\mathrm{xln}\left(\sqrt{\mathrm{2}}\right).\mathrm{e}^{−\mathrm{xln}\left(\sqrt{\mathrm{2}}\right)} =−\frac{\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\:\vee\:−\mathrm{xln}\left(\sqrt{\mathrm{2}}\right).\mathrm{e}^{−\mathrm{xln}\left(\sqrt{\mathrm{2}}\right)} =\frac{\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\Rightarrow−\mathrm{xln}\left(\sqrt{\mathrm{2}}\right)=\mathrm{W}\left(−\frac{\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\right)\vee−\mathrm{xln}\left(\sqrt{\mathrm{2}}\right)=\mathrm{W}\left(\frac{\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{ln}\left(\mathrm{2}\right)}\mathrm{W}\left(−\frac{\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\right)\vee\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{ln}\left(\mathrm{2}\right)}\mathrm{W}\left(\frac{\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\right) \\ $$$$\Rightarrow\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{ln}\left(\mathrm{2}\right)}\mathrm{W}\left(−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\approx\mathrm{6}.\mathrm{31972}\:\vee\:\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{ln}\left(\mathrm{2}\right)}\mathrm{W}\left(\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\approx−\mathrm{0}.\mathrm{578621} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com