
Question Number 187951 by chhuangakawlni last updated on 24/Feb/23
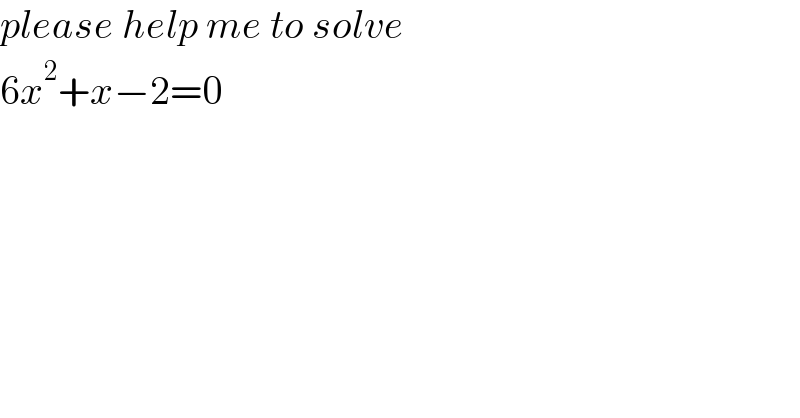
$${please}\:{help}\:{me}\:{to}\:{solve} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +{x}−\mathrm{2}=\mathrm{0} \\ $$
Answered by cortano12 last updated on 24/Feb/23

$$\left(\mathrm{x}+\frac{\mathrm{4}}{\mathrm{6}}\right)\left(\mathrm{x}−\frac{\mathrm{3}}{\mathrm{6}}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{3}}}\\{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$
Answered by Rasheed.Sindhi last updated on 24/Feb/23
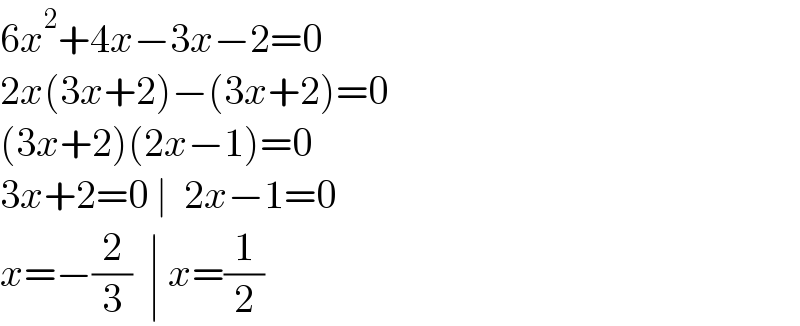
$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{3}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2}{x}\left(\mathrm{3}{x}+\mathrm{2}\right)−\left(\mathrm{3}{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\left(\mathrm{3}{x}+\mathrm{2}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{3}{x}+\mathrm{2}=\mathrm{0}\:\mid\:\:\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{2}}{\mathrm{3}}\:\:\mid\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by HeferH last updated on 25/Feb/23
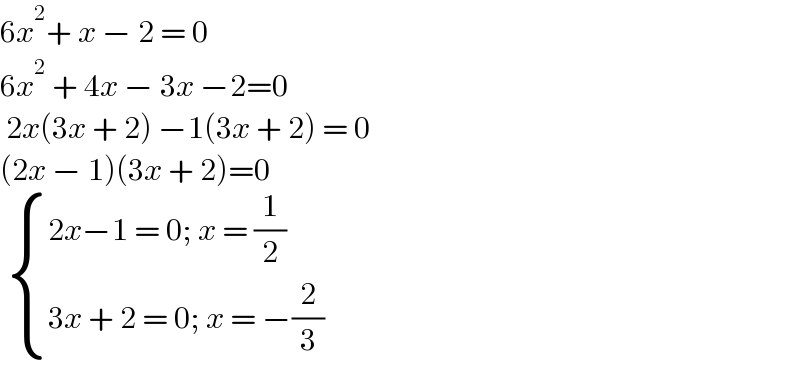
$$\mathrm{6}{x}^{\mathrm{2}} +\:{x}\:−\:\mathrm{2}\:=\:\mathrm{0} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:−\:\mathrm{3}{x}\:−\mathrm{2}=\mathrm{0} \\ $$$$\:\mathrm{2}{x}\left(\mathrm{3}{x}\:+\:\mathrm{2}\right)\:−\mathrm{1}\left(\mathrm{3}{x}\:+\:\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}{x}\:−\:\mathrm{1}\right)\left(\mathrm{3}{x}\:+\:\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{2}{x}−\mathrm{1}\:=\:\mathrm{0};\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}}\\{\mathrm{3}{x}\:+\:\mathrm{2}\:=\:\mathrm{0};\:{x}\:=\:−\frac{\mathrm{2}}{\mathrm{3}}\:}\end{cases} \\ $$
