
Question Number 46268 by Saorey last updated on 23/Oct/18
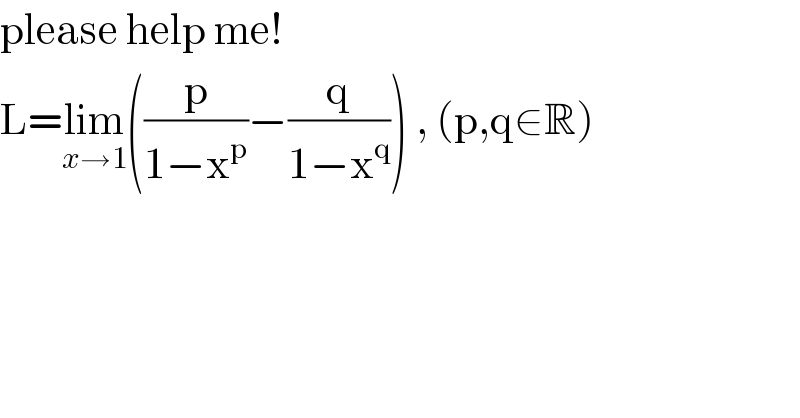
$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}! \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{p}}{\mathrm{1}−\mathrm{x}^{\mathrm{p}} }−\frac{\mathrm{q}}{\mathrm{1}−\mathrm{x}^{\mathrm{q}} }\right)\:,\:\left(\mathrm{p},\mathrm{q}\in\mathbb{R}\right) \\ $$
Commented by maxmathsup by imad last updated on 23/Oct/18
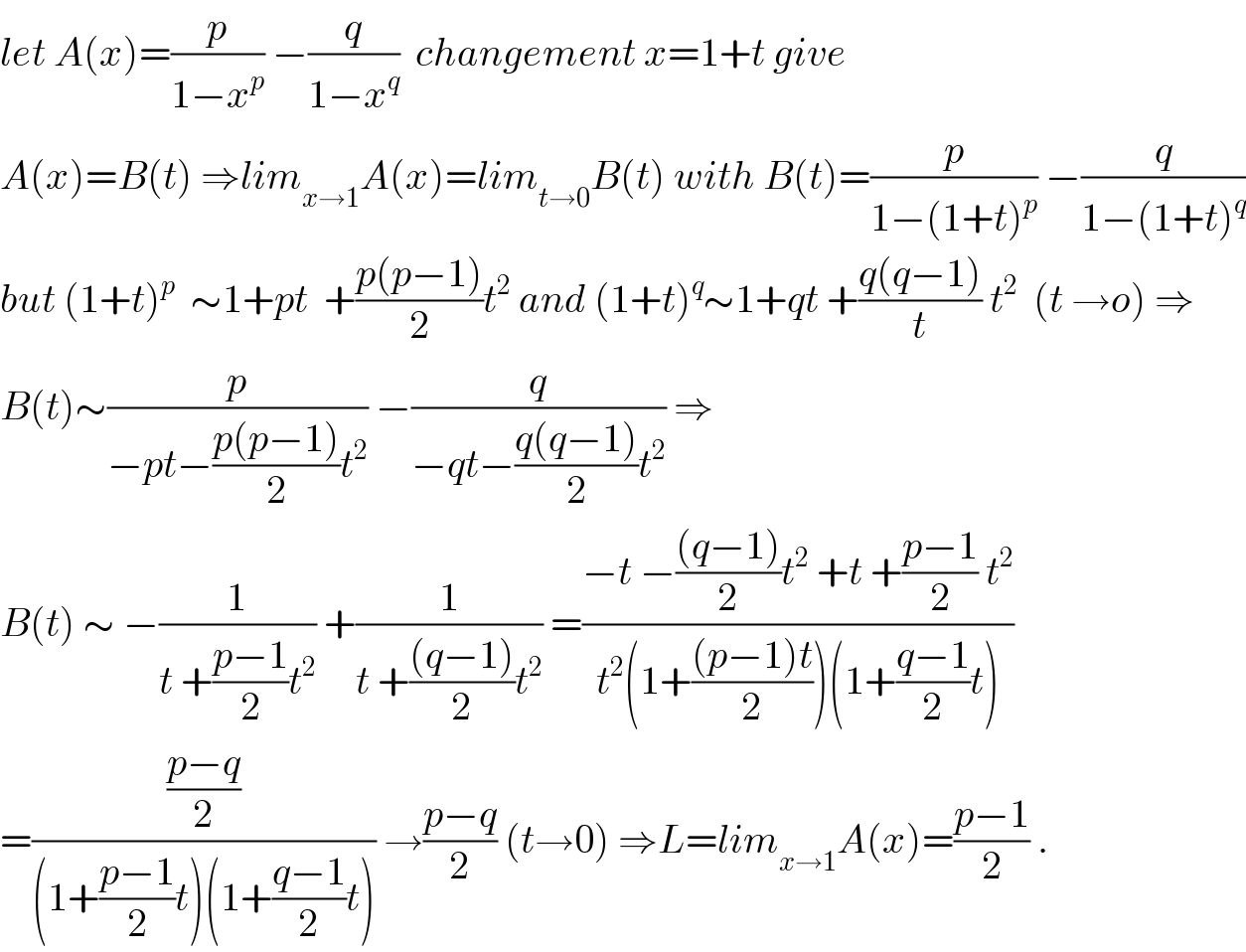
$${let}\:{A}\left({x}\right)=\frac{{p}}{\mathrm{1}−{x}^{{p}} }\:−\frac{{q}}{\mathrm{1}−{x}^{{q}} }\:\:{changement}\:{x}=\mathrm{1}+{t}\:{give} \\ $$$${A}\left({x}\right)={B}\left({t}\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} {A}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{0}} {B}\left({t}\right)\:{with}\:{B}\left({t}\right)=\frac{{p}}{\mathrm{1}−\left(\mathrm{1}+{t}\right)^{{p}} }\:−\frac{{q}}{\mathrm{1}−\left(\mathrm{1}+{t}\right)^{{q}} } \\ $$$${but}\:\left(\mathrm{1}+{t}\right)^{{p}} \:\:\sim\mathrm{1}+{pt}\:\:+\frac{{p}\left({p}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} \:{and}\:\left(\mathrm{1}+{t}\right)^{{q}} \sim\mathrm{1}+{qt}\:+\frac{{q}\left({q}−\mathrm{1}\right)}{{t}}\:{t}^{\mathrm{2}} \:\:\left({t}\:\rightarrow{o}\right)\:\Rightarrow \\ $$$${B}\left({t}\right)\sim\frac{{p}}{−{pt}−\frac{{p}\left({p}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} }\:−\frac{{q}}{−{qt}−\frac{{q}\left({q}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$${B}\left({t}\right)\:\sim\:−\frac{\mathrm{1}}{{t}\:+\frac{{p}−\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{t}\:+\frac{\left({q}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} }\:=\frac{−{t}\:−\frac{\left({q}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} \:+{t}\:+\frac{{p}−\mathrm{1}}{\mathrm{2}}\:{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left(\mathrm{1}+\frac{\left({p}−\mathrm{1}\right){t}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{{q}−\mathrm{1}}{\mathrm{2}}{t}\right)} \\ $$$$=\frac{\frac{{p}−{q}}{\mathrm{2}}}{\left(\mathrm{1}+\frac{{p}−\mathrm{1}}{\mathrm{2}}{t}\right)\left(\mathrm{1}+\frac{{q}−\mathrm{1}}{\mathrm{2}}{t}\right)}\:\rightarrow\frac{{p}−{q}}{\mathrm{2}}\:\left({t}\rightarrow\mathrm{0}\right)\:\Rightarrow{L}={lim}_{{x}\rightarrow\mathrm{1}} {A}\left({x}\right)=\frac{{p}−\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by maxmathsup by imad last updated on 23/Oct/18
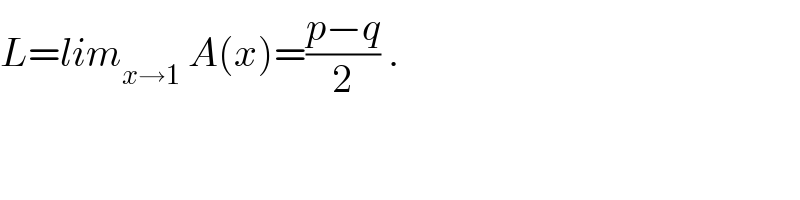
$${L}={lim}_{{x}\rightarrow\mathrm{1}} \:{A}\left({x}\right)=\frac{{p}−{q}}{\mathrm{2}}\:. \\ $$
Answered by MJS last updated on 23/Oct/18
![lim_(x→1) (p/(1−x^p ))−(q/(1−x^q ))=lim_(x→1) ((p(1−x^q )−q(1−x^p ))/((1−x^p )(1−x^q )))= [l′Hopital, 2 times because 1^(st) derivate is still undefined] =lim_(x→1) (((d^2 /dx^2 )[p(1−x^q )−q(1−x^p )])/((d^2 /dx^2 )[(1−x^p )(1−x^q )]))= =lim_(x→1) ((pq(p−1)x^(p−2) +pq(1−q)x^(q−2) )/((p+q)(p+q−1)x^(p+q−2) −p(p−1)x^(p−2) −q(q−1)x^(q−2) ))= =((p−q)/2)](Q46270.png)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{p}}{\mathrm{1}−{x}^{{p}} }−\frac{{q}}{\mathrm{1}−{x}^{{q}} }=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{p}\left(\mathrm{1}−{x}^{{q}} \right)−{q}\left(\mathrm{1}−{x}^{{p}} \right)}{\left(\mathrm{1}−{x}^{{p}} \right)\left(\mathrm{1}−{x}^{{q}} \right)}= \\ $$$$\:\:\:\:\:\left[\mathrm{l}'\mathrm{Hopital},\:\mathrm{2}\:\mathrm{times}\:\mathrm{because}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{derivate}\right. \\ $$$$\left.\:\:\:\:\:\:\mathrm{is}\:\mathrm{still}\:\mathrm{undefined}\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[{p}\left(\mathrm{1}−{x}^{{q}} \right)−{q}\left(\mathrm{1}−{x}^{{p}} \right)\right]}{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[\left(\mathrm{1}−{x}^{{p}} \right)\left(\mathrm{1}−{x}^{{q}} \right)\right]}= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{pq}\left({p}−\mathrm{1}\right){x}^{{p}−\mathrm{2}} +{pq}\left(\mathrm{1}−{q}\right){x}^{{q}−\mathrm{2}} }{\left({p}+{q}\right)\left({p}+{q}−\mathrm{1}\right){x}^{{p}+{q}−\mathrm{2}} −{p}\left({p}−\mathrm{1}\right){x}^{{p}−\mathrm{2}} −{q}\left({q}−\mathrm{1}\right){x}^{{q}−\mathrm{2}} }= \\ $$$$=\frac{{p}−{q}}{\mathrm{2}} \\ $$
Commented by Saorey last updated on 23/Oct/18
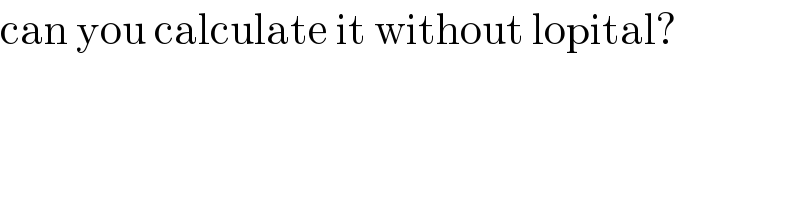
$$\mathrm{can}\:\mathrm{you}\:\mathrm{calculate}\:\mathrm{it}\:\mathrm{without}\:\mathrm{lopital}? \\ $$
Answered by ajfour last updated on 24/Oct/18
![L=lim_(x→1) {(p/(1−[1−(1−x)]^p ))−(q/(1−[1−(1−x)]^q ))} = lim_(h→0) {(p/(1−(1−ph+((p(p−1)h^2 )/2)−..)))−(q/(1−(1−qh+((q(q−1)h^2 )/2)−..)))} ⇒ L = lim_(h→0) {(1/h)[(1/(1−(((p−1)h)/2)))−(1/(1−(((q−1)h)/2)))]} = lim_(h→0) (1/h)[(((1−(((q−1)h)/2))−(1−(((p−1)h)/2)))/((1−(((p−1)h)/2))(1−(((q−1)h)/2))))] =(((((p−q)/2)))/1) =((p−q)/2) .](Q46274.png)
$${L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left\{\frac{{p}}{\mathrm{1}−\left[\mathrm{1}−\left(\mathrm{1}−{x}\right)\right]^{{p}} }−\frac{{q}}{\mathrm{1}−\left[\mathrm{1}−\left(\mathrm{1}−{x}\right)\right]^{{q}} }\right\} \\ $$$$\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{{p}}{\mathrm{1}−\left(\mathrm{1}−{ph}+\frac{{p}\left({p}−\mathrm{1}\right){h}^{\mathrm{2}} }{\mathrm{2}}−..\right)}−\frac{{q}}{\mathrm{1}−\left(\mathrm{1}−{qh}+\frac{{q}\left({q}−\mathrm{1}\right){h}^{\mathrm{2}} }{\mathrm{2}}−..\right)}\right\} \\ $$$$\Rightarrow\:\:\:{L}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{1}}{{h}}\left[\frac{\mathrm{1}}{\mathrm{1}−\frac{\left({p}−\mathrm{1}\right){h}}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\left({q}−\mathrm{1}\right){h}}{\mathrm{2}}}\right]\right\} \\ $$$$\:\:=\:\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{h}}\left[\frac{\left(\mathrm{1}−\frac{\left({q}−\mathrm{1}\right){h}}{\mathrm{2}}\right)−\left(\mathrm{1}−\frac{\left({p}−\mathrm{1}\right){h}}{\mathrm{2}}\right)}{\left(\mathrm{1}−\frac{\left({p}−\mathrm{1}\right){h}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\left({q}−\mathrm{1}\right){h}}{\mathrm{2}}\right)}\right] \\ $$$$\:\:\:\:=\frac{\left(\frac{{p}−{q}}{\mathrm{2}}\right)}{\mathrm{1}}\:\:=\frac{{p}−{q}}{\mathrm{2}}\:. \\ $$
