
Question Number 213893 by issac last updated on 21/Nov/24
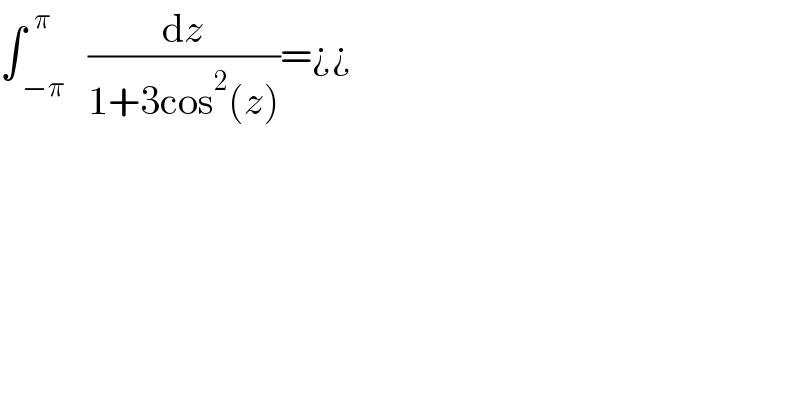
$$\int_{\:−\pi} ^{\:\:\pi} \:\:\frac{\mathrm{d}{z}}{\mathrm{1}+\mathrm{3cos}^{\mathrm{2}} \left({z}\right)}=¿¿\:\:\: \\ $$
Commented by BHOOPENDRA last updated on 21/Nov/24

$$\pi??? \\ $$
Commented by issac last updated on 21/Nov/24
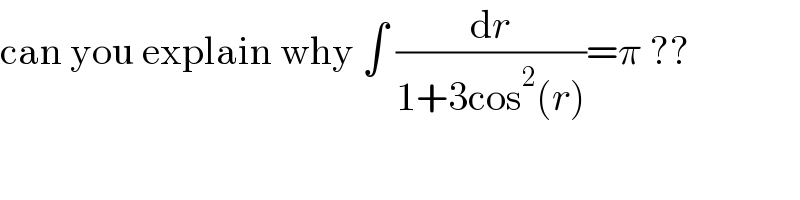
$$\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{why}\:\int\:\frac{\mathrm{d}{r}}{\mathrm{1}+\mathrm{3cos}^{\mathrm{2}} \left({r}\right)}=\pi\:?? \\ $$
Answered by mr W last updated on 21/Nov/24
![=4∫_0 ^(π/2) (dz/(1+3 cos^2 z)) =4∫_0 ^(π/2) (dz/(4−3 sin^2 z)) =(4/3)∫_0 ^(π/2) (dz/(((2/( (√3))))^2 −sin^2 z)) =2[tan^(−1) (((tan z)/2))]_0 ^(π/2) =2×(π/2)=π](Q213906.png)
$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dz}}{\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:{z}} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dz}}{\mathrm{4}−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:{z}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dz}}{\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:{z}} \\ $$$$=\mathrm{2}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:{z}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{2}×\frac{\pi}{\mathrm{2}}=\pi \\ $$
Commented by issac last updated on 21/Nov/24
$$\left.{oh}\:{u}\:{r}\:{genius}\:{thx}\::\right) \\ $$
