
Question Number 53894 by muhsangsll last updated on 27/Jan/19
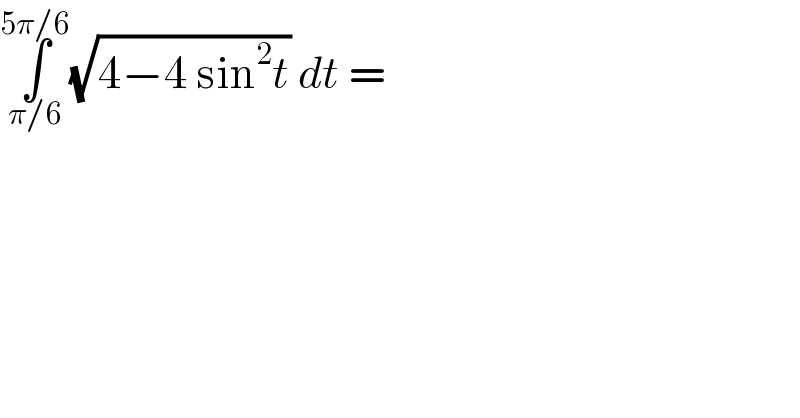
$$\underset{\pi/\mathrm{6}} {\overset{\mathrm{5}\pi/\mathrm{6}} {\int}}\sqrt{\mathrm{4}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} {t}}\:{dt}\:= \\ $$
Answered by byaw last updated on 27/Jan/19
![∫_(π/6) ^(5π/6) (√(4(1−sin^2 t))) dt ∫_(π/6) ^(5π/6) (√(4(cos^2 t))) dt ∫_(π/6) ^(5π/6) 2cost dt 2∫_(π/6) ^(5π/6) cost dt 2sin t]_(π/6) ^(5π/6) 2[sin(5π/6)−sin(π/6)] 2(1/2 −1/2) 0](Q53904.png)
$$\int_{\pi/\mathrm{6}} ^{\mathrm{5}\pi/\mathrm{6}} \sqrt{\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} {t}\right)}\:{dt} \\ $$$$\int_{\pi/\mathrm{6}} ^{\mathrm{5}\pi/\mathrm{6}} \sqrt{\mathrm{4}\left({cos}^{\mathrm{2}} {t}\right)}\:{dt} \\ $$$$\int_{\pi/\mathrm{6}} ^{\mathrm{5}\pi/\mathrm{6}} \mathrm{2}{cost}\:{dt} \\ $$$$\mathrm{2}\int_{\pi/\mathrm{6}} ^{\mathrm{5}\pi/\mathrm{6}} {cost}\:{dt} \\ $$$$\left.\mathrm{2}{sin}\:{t}\underset{\pi/\mathrm{6}} {\overset{\mathrm{5}\pi/\mathrm{6}} {\right]}} \\ $$$$\mathrm{2}\left[{sin}\left(\mathrm{5}\pi/\mathrm{6}\right)−{sin}\left(\pi/\mathrm{6}\right)\right] \\ $$$$\mathrm{2}\left(\mathrm{1}/\mathrm{2}\:−\mathrm{1}/\mathrm{2}\right) \\ $$$$\mathrm{0} \\ $$
Answered by ajfour last updated on 27/Jan/19
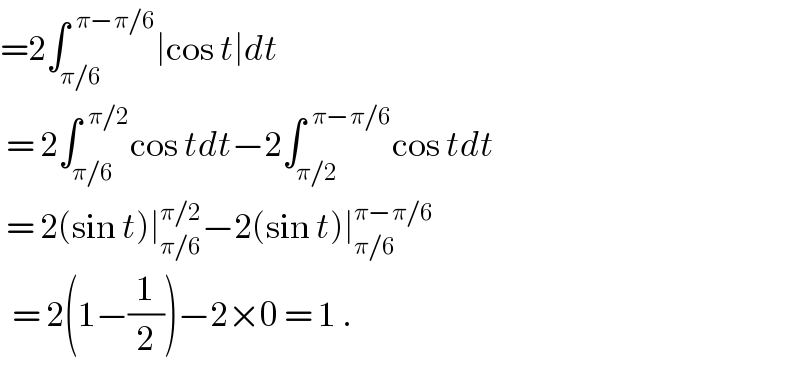
$$=\mathrm{2}\int_{\pi/\mathrm{6}} ^{\:\:\pi−\pi/\mathrm{6}} \mid\mathrm{cos}\:{t}\mid{dt}\: \\ $$$$\:=\:\mathrm{2}\int_{\pi/\mathrm{6}} ^{\:\:\pi/\mathrm{2}} \mathrm{cos}\:{tdt}−\mathrm{2}\int_{\pi/\mathrm{2}} ^{\:\:\pi−\pi/\mathrm{6}} \mathrm{cos}\:{tdt} \\ $$$$\:=\:\mathrm{2}\left(\mathrm{sin}\:{t}\right)\mid_{\pi/\mathrm{6}} ^{\pi/\mathrm{2}} −\mathrm{2}\left(\mathrm{sin}\:{t}\right)\mid_{\pi/\mathrm{6}} ^{\pi−\pi/\mathrm{6}} \\ $$$$\:\:=\:\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}×\mathrm{0}\:=\:\mathrm{1}\:. \\ $$
Commented by peter frank last updated on 27/Jan/19

$$\mathrm{p}{l}\mathrm{ease}\:\mathrm{help}\:\mathrm{53907} \\ $$
