
Question Number 88559 by 675480065 last updated on 11/Apr/20
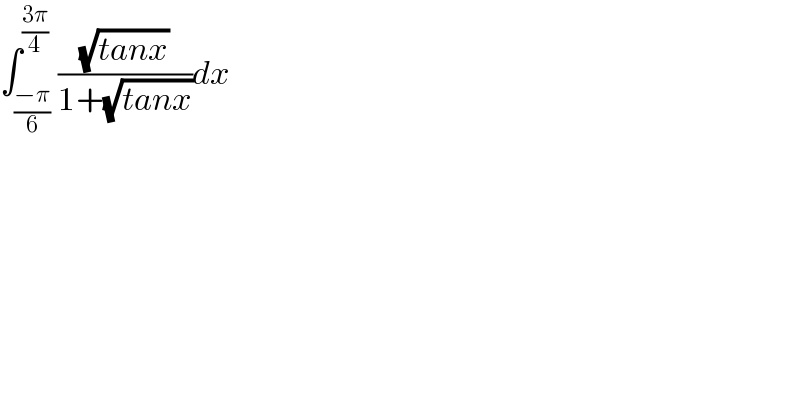
$$\int_{\frac{−\pi}{\mathrm{6}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \frac{\sqrt{{tanx}}}{\mathrm{1}+\sqrt{{tanx}}}{dx} \\ $$
Commented by MJS last updated on 11/Apr/20
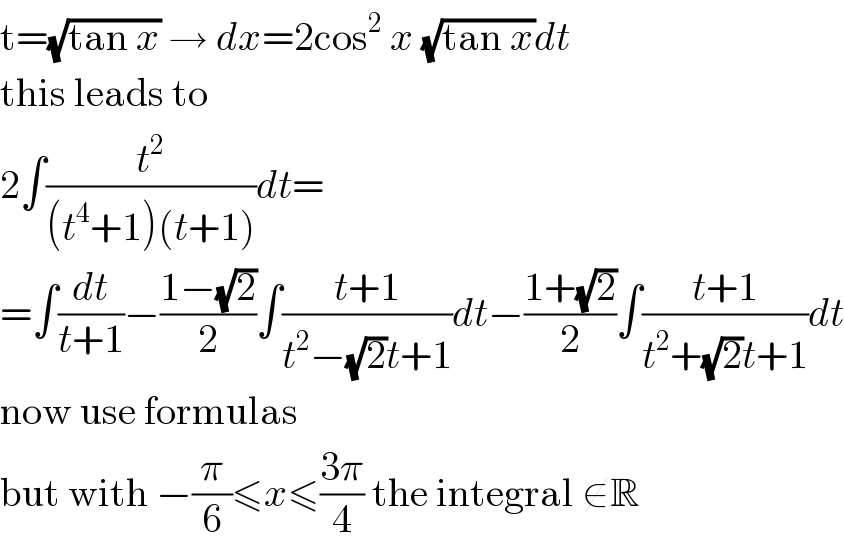
$$\mathrm{t}=\sqrt{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{2cos}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{tan}\:{x}}{dt} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{4}} +\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{dt}= \\ $$$$=\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{formulas} \\ $$$$\mathrm{but}\:\mathrm{with}\:−\frac{\pi}{\mathrm{6}}\leqslant{x}\leqslant\frac{\mathrm{3}\pi}{\mathrm{4}}\:\mathrm{the}\:\mathrm{integral}\:\notin\mathbb{R} \\ $$
