
Question Number 141387 by cesarL last updated on 18/May/21
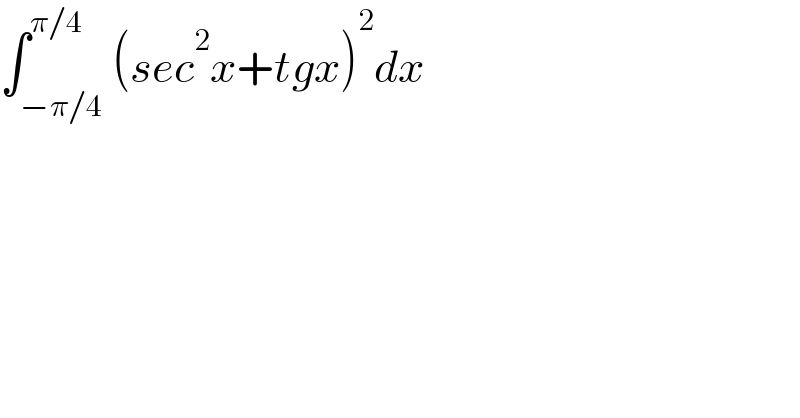
$$\int_{−\pi/\mathrm{4}} ^{\pi/\mathrm{4}} \left({sec}^{\mathrm{2}} {x}+{tgx}\right)^{\mathrm{2}} {dx} \\ $$
Answered by MJS_new last updated on 18/May/21
![∫_(−π/4) ^(π/4) (sec^2 x +tan x)^2 dx= [t=tan x → dx=cos^2 x dt] =∫_(−1) ^1 (((t^2 +t+1)^2 )/(t^2 +1))dt=∫_(−1) ^1 (t^2 +2t+2−(1/(t^2 +1)))dt= =[(t^3 /3)+t^2 +2t−arctan t]_(−1) ^1 =((14)/3)−(π/2)](Q141389.png)
$$\underset{−\pi/\mathrm{4}} {\overset{\pi/\mathrm{4}} {\int}}\left(\mathrm{sec}^{\mathrm{2}} \:{x}\:+\mathrm{tan}\:{x}\right)^{\mathrm{2}} \:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\frac{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}= \\ $$$$=\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{arctan}\:{t}\right]_{−\mathrm{1}} ^{\mathrm{1}} =\frac{\mathrm{14}}{\mathrm{3}}−\frac{\pi}{\mathrm{2}} \\ $$
