
Question Number 134420 by liberty last updated on 03/Mar/21
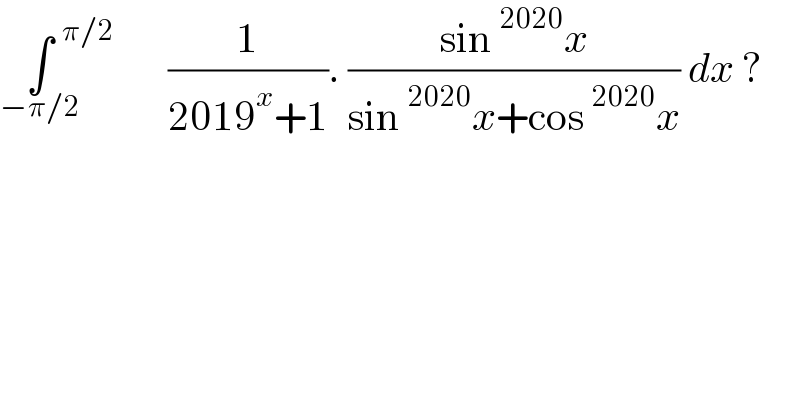
$$\underset{−\pi/\mathrm{2}} {\int}^{\:\:\:\:\:\:\pi/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2019}^{{x}} +\mathrm{1}}.\:\frac{\mathrm{sin}\:^{\mathrm{2020}} {x}}{\mathrm{sin}\:^{\mathrm{2020}} {x}+\mathrm{cos}\:^{\mathrm{2020}} {x}}\:{dx}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 03/Mar/21
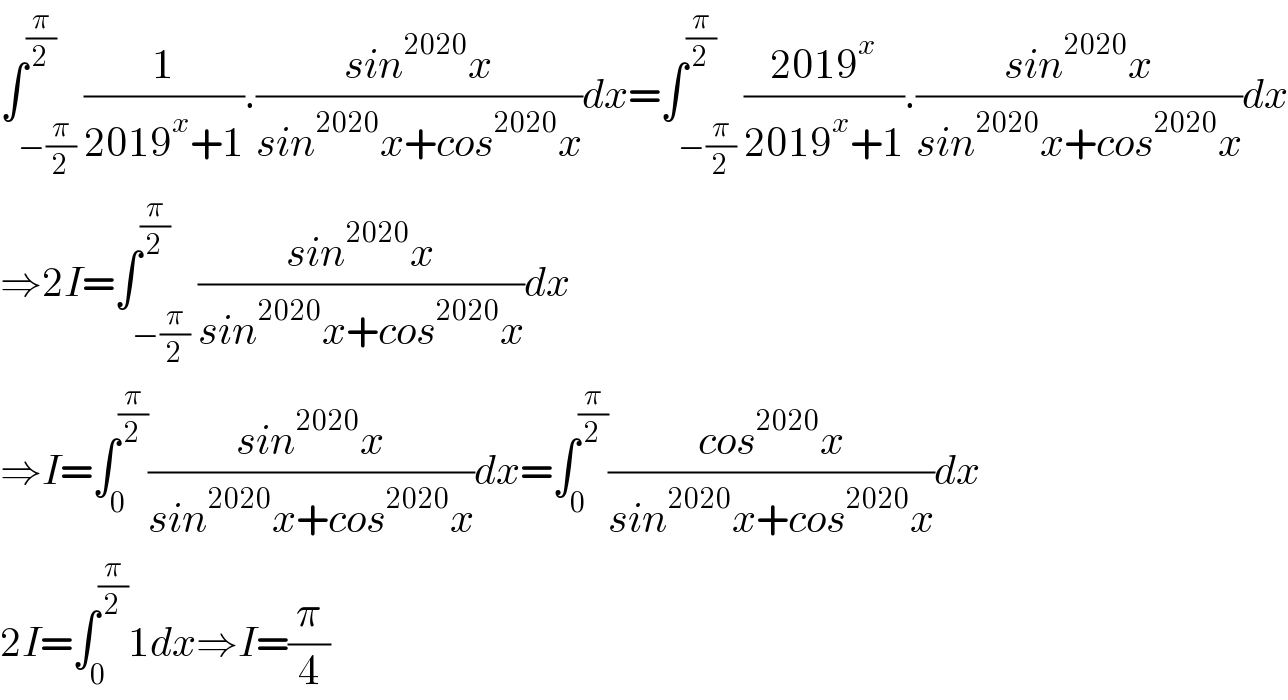
$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2019}^{{x}} +\mathrm{1}}.\frac{{sin}^{\mathrm{2020}} {x}}{{sin}^{\mathrm{2020}} {x}+{cos}^{\mathrm{2020}} {x}}{dx}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2019}^{{x}} }{\mathrm{2019}^{{x}} +\mathrm{1}}.\frac{{sin}^{\mathrm{2020}} {x}}{{sin}^{\mathrm{2020}} {x}+{cos}^{\mathrm{2020}} {x}}{dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2020}} {x}}{{sin}^{\mathrm{2020}} {x}+{cos}^{\mathrm{2020}} {x}}{dx} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2020}} {x}}{{sin}^{\mathrm{2020}} {x}+{cos}^{\mathrm{2020}} {x}}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2020}} {x}}{{sin}^{\mathrm{2020}} {x}+{cos}^{\mathrm{2020}} {x}}{dx}\: \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}{dx}\Rightarrow{I}=\frac{\pi}{\mathrm{4}} \\ $$
