
Question Number 213934 by ajfour last updated on 22/Nov/24
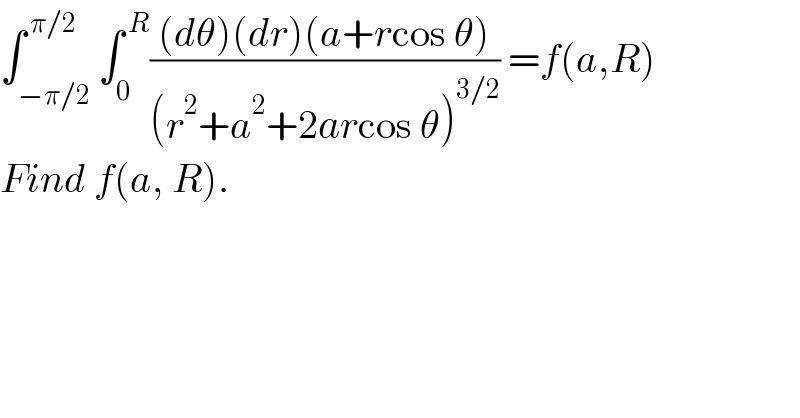
$$\int_{−\pi/\mathrm{2}} ^{\:\pi/\mathrm{2}} \int_{\mathrm{0}} ^{\:{R}} \frac{\left({d}\theta\right)\left({dr}\right)\left({a}+{r}\mathrm{cos}\:\theta\right)}{\left({r}^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{ar}\mathrm{cos}\:\theta\right)^{\mathrm{3}/\mathrm{2}} }\:={f}\left({a},{R}\right) \\ $$$${Find}\:{f}\left({a},\:{R}\right). \\ $$
Commented by ajfour last updated on 23/Nov/24
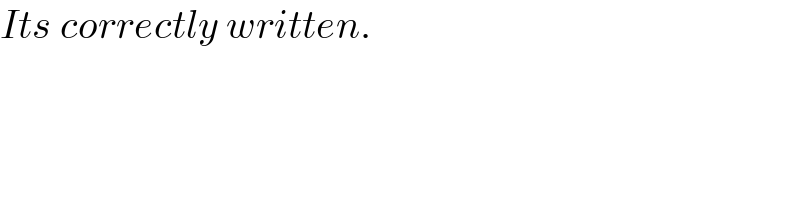
$${Its}\:{correctly}\:{written}. \\ $$
Commented by ajfour last updated on 23/Nov/24
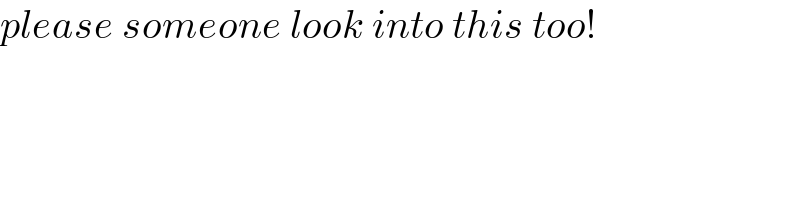
$${please}\:{someone}\:{look}\:{into}\:{this}\:{too}! \\ $$
Commented by BHOOPENDRA last updated on 23/Nov/24
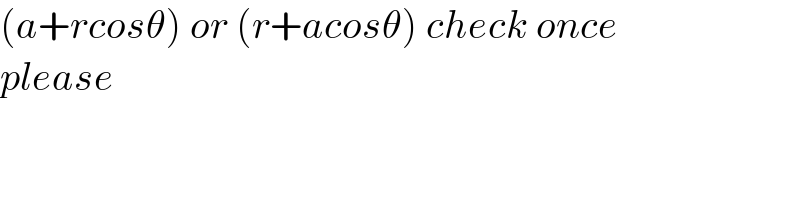
$$\left({a}+{rcos}\theta\right)\:{or}\:\left({r}+{acos}\theta\right)\:{check}\:{once} \\ $$$${please}\: \\ $$
