
Question Number 183320 by mathlove last updated on 25/Dec/22
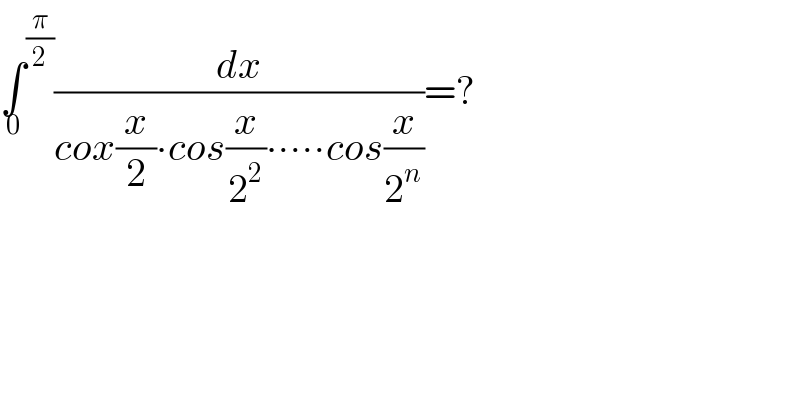
$$\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{cox}\frac{{x}}{\mathrm{2}}\centerdot{cos}\frac{{x}}{\mathrm{2}^{\mathrm{2}} }\centerdot\centerdot\centerdot\centerdot\centerdot{cos}\frac{{x}}{\mathrm{2}^{{n}} }}=? \\ $$
Answered by Vynho last updated on 28/Dec/22
![∫_0 ^(π/2) (dx/(Π_(k=1) ^n cos((x/2^k )))) ln(Π_(k=1) ^n cos((x/2^k )))=Σ_(k=1) ^n ln(cos((x/2^k ))) Π_(k=1) ^n cos((x/a^k ))+isin((x/a^k ))=Π_(k=1) ^n e^(i(x/a^k )) U_n =Π_(k=1) ^n e^(ix((1/a))^k ) ln(U_n )=Σ_(k=1) ^n ln(e^(ix((1/a))^k ) )=ixΣ_(k=1) ^n ((1/a))^k ln(U_n )=ix(1/a).((1−((1/a))^n )/(1−(1/a)))=ix.((1−((1/a))^n )/(a−1)) U_n =e^(ix((1−((1/a))^n )/(a−1))) ∫_0 ^(π/2) e^(−ix((1−((1/a))^n )/(a−1))) dx=∫_0 ^(π/2) e^(−ixθ) dx=(1/(−iθ))[e^(−ixθ) ]_0 ^(π/2) I=(i/θ)[e^(−i(π/2)θ) −1]=(1/θ)[icos((π/2)θ)+sin((π/2)θ)] ∫_0 ^(π/2) (dx/(Π_(k=1) ^n cos((x/2^k ))))=(1/θ)sin((π/2)θ) θ=((1−((1/a))^n )/(a−1))](Q183670.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)} \\ $$$${ln}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left({cos}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left(\frac{{x}}{{a}^{{k}} }\right)+{isin}\left(\frac{{x}}{{a}^{{k}} }\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{e}^{{i}\frac{{x}}{{a}^{{k}} }} \\ $$$${U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{e}^{{ix}\left(\frac{\mathrm{1}}{{a}}\right)^{{k}} } \\ $$$${ln}\left({U}_{{n}} \right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left({e}^{{ix}\left(\frac{\mathrm{1}}{{a}}\right)^{{k}} } \right)={ix}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{a}}\right)^{{k}} \\ $$$$ \\ $$$${ln}\left({U}_{{n}} \right)={ix}\frac{\mathrm{1}}{{a}}.\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{{a}}\right)^{{n}} }{\mathrm{1}−\frac{\mathrm{1}}{{a}}}={ix}.\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{{a}}\right)^{{n}} }{{a}−\mathrm{1}} \\ $$$${U}_{{n}} ={e}^{{ix}\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{{a}}\right)^{{n}} }{{a}−\mathrm{1}}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {e}^{−{ix}\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{{a}}\right)^{{n}} }{{a}−\mathrm{1}}} {dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {e}^{−{ix}\theta} {dx}=\frac{\mathrm{1}}{−{i}\theta}\left[{e}^{−{ix}\theta} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$${I}=\frac{{i}}{\theta}\left[{e}^{−{i}\frac{\pi}{\mathrm{2}}\theta} −\mathrm{1}\right]=\frac{\mathrm{1}}{\theta}\left[{icos}\left(\frac{\pi}{\mathrm{2}}\theta\right)+{sin}\left(\frac{\pi}{\mathrm{2}}\theta\right)\right] \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)}=\frac{\mathrm{1}}{\theta}{sin}\left(\frac{\pi}{\mathrm{2}}\theta\right)\: \\ $$$$\theta=\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{{a}}\right)^{{n}} }{{a}−\mathrm{1}} \\ $$
Commented by Vynho last updated on 28/Dec/22

$${a}=\mathrm{2} \\ $$
Commented by mathlove last updated on 03/Jan/23

$${thanks} \\ $$
