
Question Number 200085 by a.lgnaoui last updated on 13/Nov/23
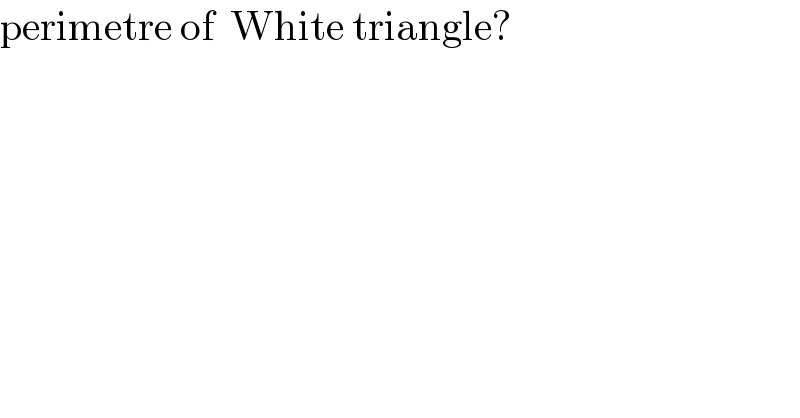
$$\mathrm{perimetre}\:\mathrm{of}\:\:\mathrm{White}\:\mathrm{triangle}? \\ $$
Commented by a.lgnaoui last updated on 13/Nov/23
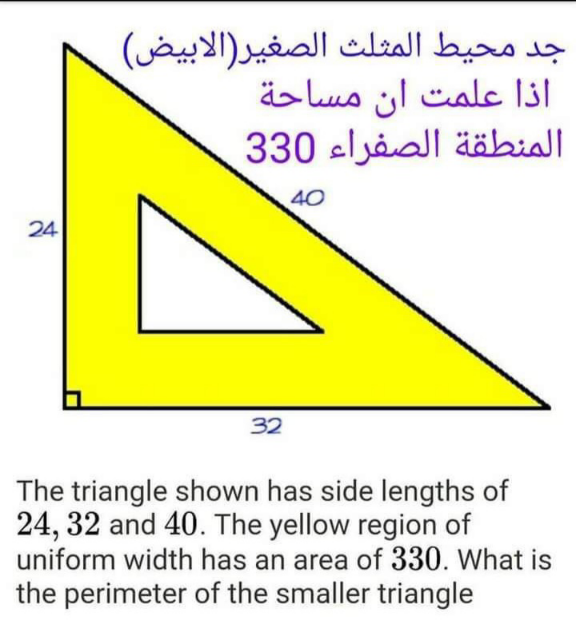
Commented by Nimnim111118 last updated on 13/Nov/23
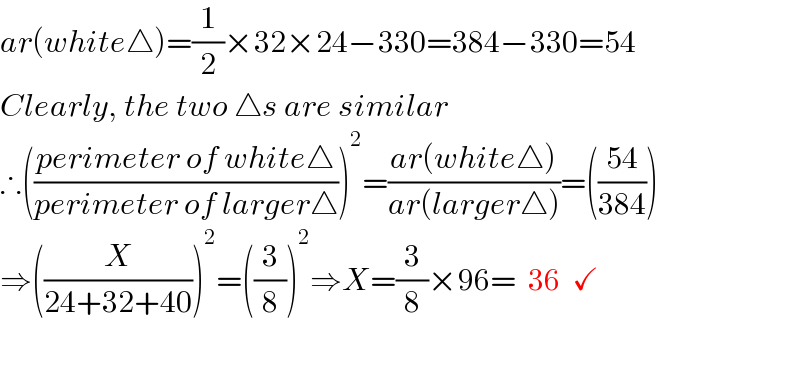
$${ar}\left({white}\bigtriangleup\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{32}×\mathrm{24}−\mathrm{330}=\mathrm{384}−\mathrm{330}=\mathrm{54} \\ $$$${Clearly},\:{the}\:{two}\:\bigtriangleup{s}\:{are}\:{similar} \\ $$$$\therefore\left(\frac{{perimeter}\:{of}\:{white}\bigtriangleup}{{perimeter}\:{of}\:{larger}\bigtriangleup}\right)^{\mathrm{2}} =\frac{{ar}\left({white}\bigtriangleup\right)}{{ar}\left({larger}\bigtriangleup\right)}=\left(\frac{\mathrm{54}}{\mathrm{384}}\right) \\ $$$$\Rightarrow\left(\frac{{X}}{\mathrm{24}+\mathrm{32}+\mathrm{40}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{2}} \Rightarrow{X}=\frac{\mathrm{3}}{\mathrm{8}}×\mathrm{96}=\:\:\mathrm{36}\:\:\checkmark \\ $$$$ \\ $$
Answered by mr W last updated on 13/Nov/23
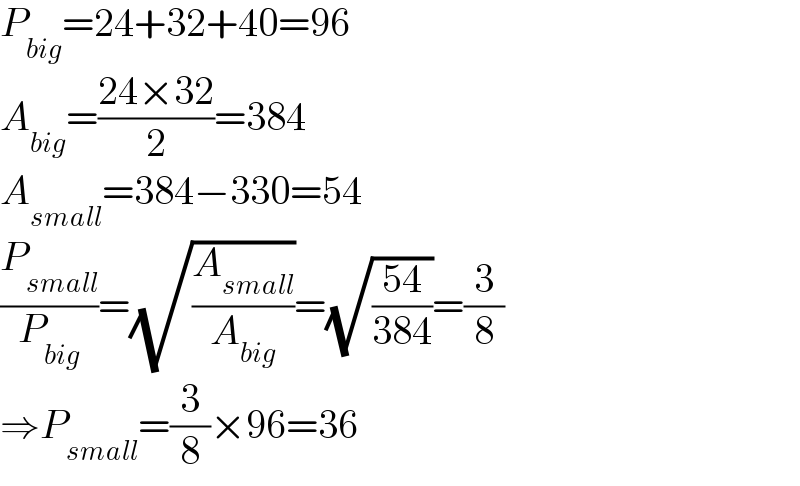
$${P}_{{big}} =\mathrm{24}+\mathrm{32}+\mathrm{40}=\mathrm{96} \\ $$$${A}_{{big}} =\frac{\mathrm{24}×\mathrm{32}}{\mathrm{2}}=\mathrm{384} \\ $$$${A}_{{small}} =\mathrm{384}−\mathrm{330}=\mathrm{54} \\ $$$$\frac{{P}_{{small}} }{{P}_{{big}} }=\sqrt{\frac{{A}_{{small}} }{{A}_{{big}} }}=\sqrt{\frac{\mathrm{54}}{\mathrm{384}}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\Rightarrow{P}_{{small}} =\frac{\mathrm{3}}{\mathrm{8}}×\mathrm{96}=\mathrm{36} \\ $$
