
Question Number 103832 by bemath last updated on 17/Jul/20
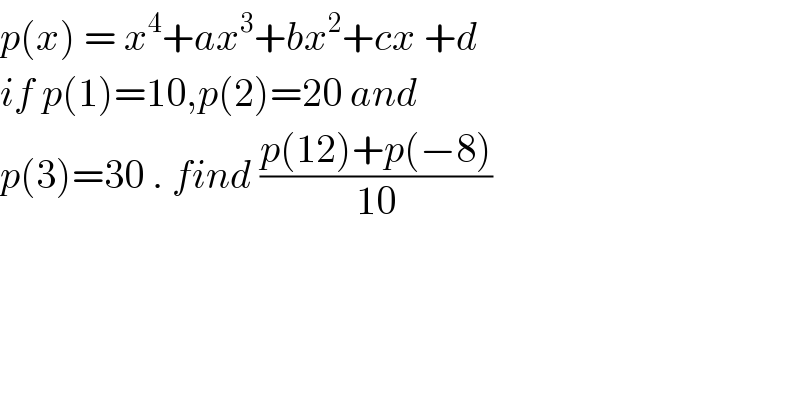
$${p}\left({x}\right)\:=\:{x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}\:+{d} \\ $$$${if}\:{p}\left(\mathrm{1}\right)=\mathrm{10},{p}\left(\mathrm{2}\right)=\mathrm{20}\:{and} \\ $$$${p}\left(\mathrm{3}\right)=\mathrm{30}\:.\:{find}\:\frac{{p}\left(\mathrm{12}\right)+{p}\left(−\mathrm{8}\right)}{\mathrm{10}} \\ $$
Answered by floor(10²Eta[1]) last updated on 17/Jul/20
![p(x)=(x−1)(x−2)(x−3)(x−x_4 )+10x p(12)=11.10.9(12−x_4 )+120 p(−8)=(−9)(−10)(−11)(−8−x_4 )−80 ((p(12)+p(−8))/(10))=99(12−x_4 )+12−99(−8−x_4 )−8 =99[(12−x_4 )−(−8−x_4 )]+4=99.20+4=1984](Q103855.png)
$$\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}−\mathrm{x}_{\mathrm{4}} \right)+\mathrm{10x} \\ $$$$\mathrm{p}\left(\mathrm{12}\right)=\mathrm{11}.\mathrm{10}.\mathrm{9}\left(\mathrm{12}−\mathrm{x}_{\mathrm{4}} \right)+\mathrm{120} \\ $$$$\mathrm{p}\left(−\mathrm{8}\right)=\left(−\mathrm{9}\right)\left(−\mathrm{10}\right)\left(−\mathrm{11}\right)\left(−\mathrm{8}−\mathrm{x}_{\mathrm{4}} \right)−\mathrm{80} \\ $$$$\frac{\mathrm{p}\left(\mathrm{12}\right)+\mathrm{p}\left(−\mathrm{8}\right)}{\mathrm{10}}=\mathrm{99}\left(\mathrm{12}−\mathrm{x}_{\mathrm{4}} \right)+\mathrm{12}−\mathrm{99}\left(−\mathrm{8}−\mathrm{x}_{\mathrm{4}} \right)−\mathrm{8} \\ $$$$=\mathrm{99}\left[\left(\mathrm{12}−\mathrm{x}_{\mathrm{4}} \right)−\left(−\mathrm{8}−\mathrm{x}_{\mathrm{4}} \right)\right]+\mathrm{4}=\mathrm{99}.\mathrm{20}+\mathrm{4}=\mathrm{1984} \\ $$$$ \\ $$
