
Question Number 144060 by Khalmohmmad last updated on 21/Jun/21
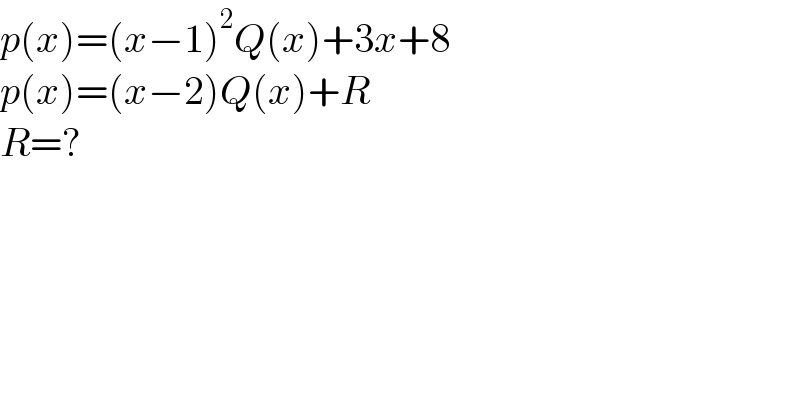
$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {Q}\left({x}\right)+\mathrm{3}{x}+\mathrm{8} \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{2}\right){Q}\left({x}\right)+{R} \\ $$$${R}=? \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jun/21

$${Q}\left({x}\right)\:{is}\:{same}\:{in}\:{both}\:{cases}!!!? \\ $$
Answered by Rasheed.Sindhi last updated on 21/Jun/21
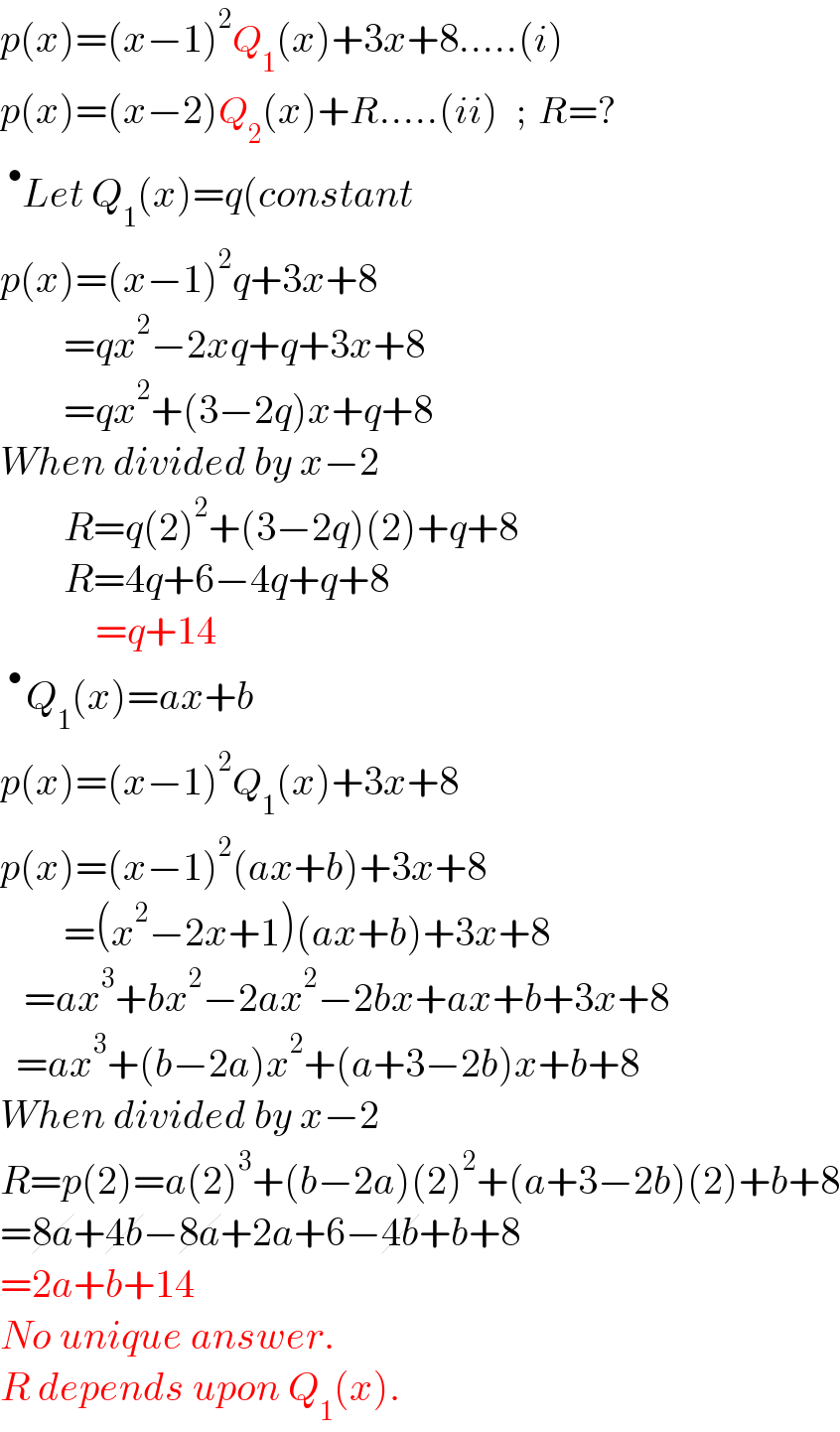
$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {Q}_{\mathrm{1}} \left({x}\right)+\mathrm{3}{x}+\mathrm{8}.....\left({i}\right) \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{2}\right){Q}_{\mathrm{2}} \left({x}\right)+{R}.....\left({ii}\right)\:\:\:;\:\:{R}=? \\ $$$$\:^{\bullet} {Let}\:{Q}_{\mathrm{1}} \left({x}\right)={q}\left({constant}\right. \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {q}+\mathrm{3}{x}+\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:={qx}^{\mathrm{2}} −\mathrm{2}{xq}+{q}+\mathrm{3}{x}+\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:={qx}^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{2}{q}\right){x}+{q}+\mathrm{8} \\ $$$${When}\:{divided}\:{by}\:{x}−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:{R}={q}\left(\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{2}{q}\right)\left(\mathrm{2}\right)+{q}+\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:{R}=\mathrm{4}{q}+\mathrm{6}−\mathrm{4}{q}+{q}+\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={q}+\mathrm{14} \\ $$$$\:^{\bullet\:} {Q}_{\mathrm{1}} \left({x}\right)={ax}+{b}\:\:\:\: \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {Q}_{\mathrm{1}} \left({x}\right)+\mathrm{3}{x}+\mathrm{8} \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({ax}+{b}\right)+\mathrm{3}{x}+\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:=\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)\left({ax}+{b}\right)+\mathrm{3}{x}+\mathrm{8} \\ $$$$\:\:\:={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} −\mathrm{2}{ax}^{\mathrm{2}} −\mathrm{2}{bx}+{ax}+{b}+\mathrm{3}{x}+\mathrm{8} \\ $$$$\:\:={ax}^{\mathrm{3}} +\left({b}−\mathrm{2}{a}\right){x}^{\mathrm{2}} +\left({a}+\mathrm{3}−\mathrm{2}{b}\right){x}+{b}+\mathrm{8} \\ $$$${When}\:{divided}\:{by}\:{x}−\mathrm{2} \\ $$$${R}={p}\left(\mathrm{2}\right)={a}\left(\mathrm{2}\right)^{\mathrm{3}} +\left({b}−\mathrm{2}{a}\right)\left(\mathrm{2}\right)^{\mathrm{2}} +\left({a}+\mathrm{3}−\mathrm{2}{b}\right)\left(\mathrm{2}\right)+{b}+\mathrm{8} \\ $$$$=\cancel{\mathrm{8}{a}}+\cancel{\mathrm{4}{b}}−\cancel{\mathrm{8}{a}}+\mathrm{2}{a}+\mathrm{6}−\cancel{\mathrm{4}{b}}+{b}+\mathrm{8} \\ $$$$=\mathrm{2}{a}+{b}+\mathrm{14} \\ $$$${No}\:{unique}\:{answer}. \\ $$$${R}\:{depends}\:{upon}\:{Q}_{\mathrm{1}} \left({x}\right). \\ $$
Answered by Rasheed.Sindhi last updated on 21/Jun/21

$${p}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} {Q}_{\mathrm{1}} \left({x}\right)+\mathrm{3}{x}+\mathrm{8} \\ $$$${p}\left({x}\right)=\left({x}−\mathrm{2}\right){Q}_{\mathrm{2}} \left({x}\right)+{R}\:\:;\:\:{R}=? \\ $$$${p}\left({x}\right)\:{when}\:{is}\:{divided}\:{by}\:{x}−\mathrm{2}\:{giving}\: \\ $$$${remainder}\:{R} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} {Q}_{\mathrm{1}} \left({x}\right)+\mathrm{3}{x}+\mathrm{8}\:\:{is}\:{divided}\:{by} \\ $$$${x}−\mathrm{2}\:{giving}\:{remainder}\:{R} \\ $$$${R}={p}\left(\mathrm{2}\right)=\left(\mathrm{2}−\mathrm{1}\right)^{\mathrm{2}} {Q}_{\mathrm{1}} \left(\mathrm{2}\right)+\mathrm{3}\left(\mathrm{2}\right)+\mathrm{8} \\ $$$${R}={p}\left(\mathrm{2}\right)={Q}_{\mathrm{1}} \left(\mathrm{2}\right)+\mathrm{14} \\ $$$$\:^{\bullet} {Let}\:\:{Q}_{\mathrm{1}} \left({x}\right)={q}\:\left({constant}\right) \\ $$$${R}={q}+\mathrm{14} \\ $$$$\:^{\bullet} {Let}\:{Q}_{\mathrm{1}} \left({x}\right)={ax}+{b} \\ $$$${R}={Q}_{\mathrm{1}} \left(\mathrm{2}\right)+\mathrm{14}={a}\left(\mathrm{2}\right)+{b}+\mathrm{14} \\ $$$$\:\:\:\:\:\:\:\:\:\:{R}=\mathrm{2}{a}+{b}+\mathrm{14} \\ $$$$\:^{\bullet} {Let}\:{Q}_{\mathrm{1}} \left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$$\:\:\:\:{R}={a}\left(\mathrm{2}\right)^{\mathrm{2}} +{b}\left(\mathrm{2}\right)+{c}+\mathrm{14} \\ $$$$\:\:\:\:\:\:\:{R}=\mathrm{4}{a}+\mathrm{2}{b}+{c}+\mathrm{14} \\ $$$${R}\:{depends}\:{on}\:{Q}_{\mathrm{1}} \left({x}\right)\:\left({or}\:{Q}_{\mathrm{2}} \left({x}\right)\:\right). \\ $$$${It}'{s}\:{not}\:{unique}. \\ $$$$ \\ $$
