
Question Number 129090 by Adel last updated on 12/Jan/21
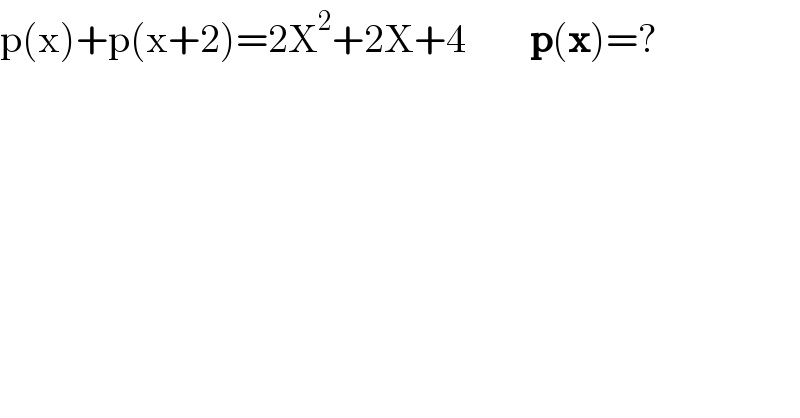
$$\mathrm{p}\left(\mathrm{x}\right)+\mathrm{p}\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{2X}^{\mathrm{2}} +\mathrm{2X}+\mathrm{4}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{p}}\left(\boldsymbol{\mathrm{x}}\right)=? \\ $$
Answered by MJS_new last updated on 12/Jan/21
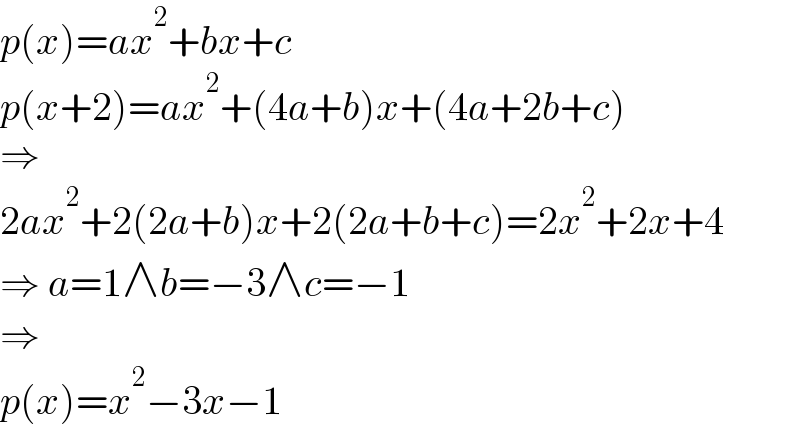
$${p}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${p}\left({x}+\mathrm{2}\right)={ax}^{\mathrm{2}} +\left(\mathrm{4}{a}+{b}\right){x}+\left(\mathrm{4}{a}+\mathrm{2}{b}+{c}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2}{ax}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}{a}+{b}\right){x}+\mathrm{2}\left(\mathrm{2}{a}+{b}+{c}\right)=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4} \\ $$$$\Rightarrow\:{a}=\mathrm{1}\wedge{b}=−\mathrm{3}\wedge{c}=−\mathrm{1} \\ $$$$\Rightarrow \\ $$$${p}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{1} \\ $$
Commented by Adel last updated on 12/Jan/21

$$\mathrm{tanks} \\ $$
