
Question Number 177856 by mathlove last updated on 10/Oct/22
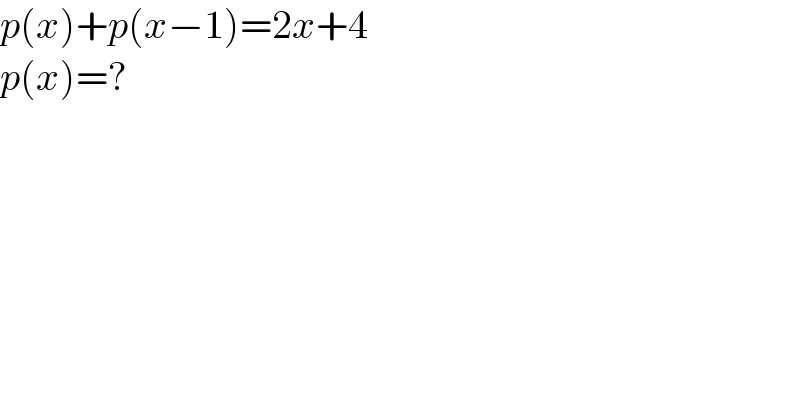
$${p}\left({x}\right)+{p}\left({x}−\mathrm{1}\right)=\mathrm{2}{x}+\mathrm{4} \\ $$$${p}\left({x}\right)=? \\ $$
Answered by blackmamba last updated on 10/Oct/22
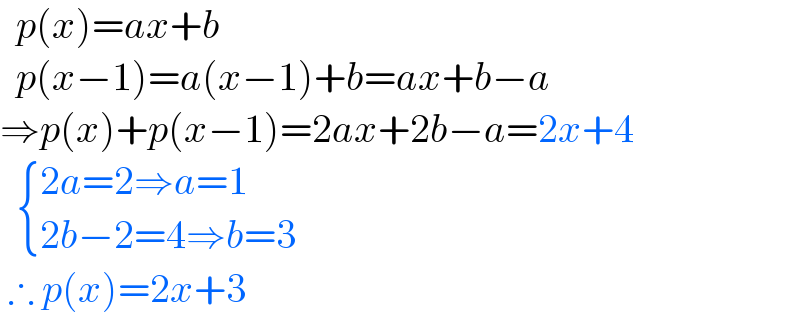
$$\:\:{p}\left({x}\right)={ax}+{b}\: \\ $$$$\:\:{p}\left({x}−\mathrm{1}\right)={a}\left({x}−\mathrm{1}\right)+{b}={ax}+{b}−{a} \\ $$$$\Rightarrow{p}\left({x}\right)+{p}\left({x}−\mathrm{1}\right)=\mathrm{2}{ax}+\mathrm{2}{b}−{a}=\mathrm{2}{x}+\mathrm{4} \\ $$$$\:\:\begin{cases}{\mathrm{2}{a}=\mathrm{2}\Rightarrow{a}=\mathrm{1}}\\{\mathrm{2}{b}−\mathrm{2}=\mathrm{4}\Rightarrow{b}=\mathrm{3}}\end{cases} \\ $$$$\:\therefore\:{p}\left({x}\right)=\mathrm{2}{x}+\mathrm{3} \\ $$
Commented by mathlove last updated on 10/Oct/22

$${thanks} \\ $$
Commented by Tinku Tara last updated on 10/Oct/22

$$\mathrm{Small}\:\mathrm{caculation}\:\mathrm{error}.\:\mathrm{pls}\:\mathrm{check} \\ $$$${a}=\mathrm{1} \\ $$$$\mathrm{2}{b}−{a}=\mathrm{4}\Rightarrow{b}=\mathrm{2}.\mathrm{5} \\ $$$${p}\left({x}\right)=\mathrm{2}{x}+\mathrm{2}.\mathrm{5} \\ $$
