
Question Number 179890 by mr W last updated on 03/Nov/22
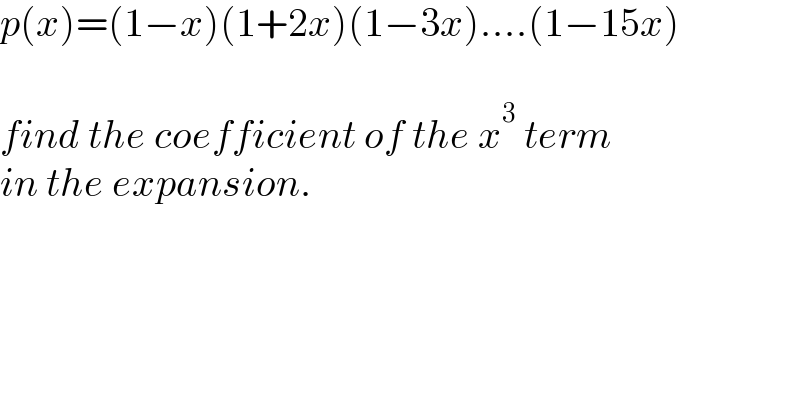
$${p}\left({x}\right)=\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{1}−\mathrm{3}{x}\right)....\left(\mathrm{1}−\mathrm{15}{x}\right) \\ $$$$ \\ $$$${find}\:{the}\:{coefficient}\:{of}\:{the}\:{x}^{\mathrm{3}} \:{term} \\ $$$${in}\:{the}\:{expansion}. \\ $$
Commented by mr W last updated on 03/Nov/22

$${adapted}\:{from}\:{Q}\mathrm{179777} \\ $$
Answered by mr W last updated on 04/Nov/22
![Method II we need these values later: Σ_(k=1) ^(15) (−1)^k k=−(1+3+5+...+15)+(2+4+...+14) =−((8×16)/2)+((7×16)/2)=−8 Σ_(k=1) ^(15) k^2 =1^2 +2^2 +...+15^2 =((15×(15+1)(2×15+1))/6)=1240 Σ_(k=1) ^(15) (−1)^k k^3 =Σ_(m=0) ^7 [−(2m+1)^3 +(2m)^3 ] =Σ_(m=0) ^7 [−3(2m)^2 −3(2m)−1] =−Σ_(m=0) ^7 [12m^2 +6m+1] =−[12×((7×(7+1)×(2×7+1))/6)+6×((7×8)/2)+8] =−1856 as we have calculated in an other question the coef. of x^2 in p(x) is −588. the coef. of x^3 in p(x) is (1/3)Σ_(k=1) ^(15) (−1)^k k×[coef. of x^2 in ((p(x))/(1+(−1)^k kx))] =(1/3)Σ_(k=1) ^(15) (−1)^k k×[coef. of x^2 in {p(x)−(−1)^k kxp(x)+(−1)^(2k) k^2 x^2 p(x)−...}] =(1/3)Σ_(k=1) ^(15) (−1)^k k×[−588−(−1)^k kΣ_(r=1) ^(15) (−1)^r r+k^2 ] =(1/3)Σ_(k=1) ^(15) (−1)^k k×[−588+8(−1)^k k+k^2 ] =(1/3)Σ_(k=1) ^(15) [−588(−1)^k k+8k^2 +(−1)^k k^3 ] =(1/3)[588×8+8×1240−1856] =(1/3)[12768] =4256](Q179924.png)
$$\boldsymbol{{Method}}\:\boldsymbol{{II}} \\ $$$${we}\:{need}\:{these}\:{values}\:{later}: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {k}=−\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+...+\mathrm{15}\right)+\left(\mathrm{2}+\mathrm{4}+...+\mathrm{14}\right) \\ $$$$\:\:\:\:\:\:\:\:=−\frac{\mathrm{8}×\mathrm{16}}{\mathrm{2}}+\frac{\mathrm{7}×\mathrm{16}}{\mathrm{2}}=−\mathrm{8} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}{k}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +...+\mathrm{15}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{15}×\left(\mathrm{15}+\mathrm{1}\right)\left(\mathrm{2}×\mathrm{15}+\mathrm{1}\right)}{\mathrm{6}}=\mathrm{1240} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {k}^{\mathrm{3}} =\underset{{m}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\left[−\left(\mathrm{2}{m}+\mathrm{1}\right)^{\mathrm{3}} +\left(\mathrm{2}{m}\right)^{\mathrm{3}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{{m}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\left[−\mathrm{3}\left(\mathrm{2}{m}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{2}{m}\right)−\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:=−\underset{{m}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\left[\mathrm{12}{m}^{\mathrm{2}} +\mathrm{6}{m}+\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:=−\left[\mathrm{12}×\frac{\mathrm{7}×\left(\mathrm{7}+\mathrm{1}\right)×\left(\mathrm{2}×\mathrm{7}+\mathrm{1}\right)}{\mathrm{6}}+\mathrm{6}×\frac{\mathrm{7}×\mathrm{8}}{\mathrm{2}}+\mathrm{8}\right] \\ $$$$\:\:\:\:\:\:\:\:\:=−\mathrm{1856} \\ $$$$ \\ $$$${as}\:{we}\:{have}\:{calculated}\:{in}\:{an}\:{other} \\ $$$${question}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{2}} \:{in}\:{p}\left({x}\right)\:{is}\: \\ $$$$−\mathrm{588}. \\ $$$$ \\ $$$${the}\:{coef}.\:{of}\:{x}^{\mathrm{3}} \:{in}\:{p}\left({x}\right)\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {k}×\left[{coef}.\:{of}\:{x}^{\mathrm{2}} \:{in}\:\frac{{p}\left({x}\right)}{\mathrm{1}+\left(−\mathrm{1}\right)^{{k}} {kx}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {k}×\left[{coef}.\:{of}\:{x}^{\mathrm{2}} \:{in}\:\left\{{p}\left({x}\right)−\left(−\mathrm{1}\right)^{{k}} {kxp}\left({x}\right)+\left(−\mathrm{1}\right)^{\mathrm{2}{k}} {k}^{\mathrm{2}} {x}^{\mathrm{2}} {p}\left({x}\right)−...\right\}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {k}×\left[−\mathrm{588}−\left(−\mathrm{1}\right)^{{k}} {k}\underset{{r}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{r}} {r}+{k}^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {k}×\left[−\mathrm{588}+\mathrm{8}\left(−\mathrm{1}\right)^{{k}} {k}+{k}^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left[−\mathrm{588}\left(−\mathrm{1}\right)^{{k}} {k}+\mathrm{8}{k}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{{k}} {k}^{\mathrm{3}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{588}×\mathrm{8}+\mathrm{8}×\mathrm{1240}−\mathrm{1856}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{12768}\right] \\ $$$$=\mathrm{4256} \\ $$
Commented by mr W last updated on 04/Nov/22
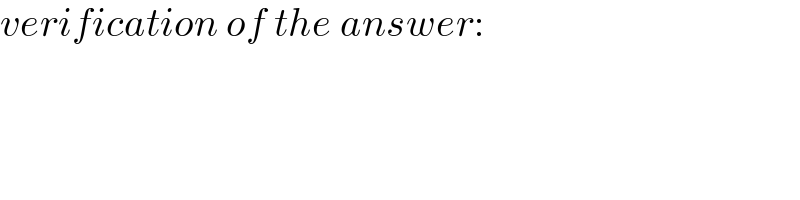
$${verification}\:{of}\:{the}\:{answer}: \\ $$
Commented by mr W last updated on 04/Nov/22

Answered by mr W last updated on 04/Nov/22

$$\boldsymbol{{Method}}\:\boldsymbol{{I}} \\ $$$${basically}\:{we}\:{just}\:{calculate}\:{the}\:{sum} \\ $$$${of}\:{all}\:{possible}\:{products}\:{from}\:{a},{b},{c} \\ $$$${with}\:{a},{b},{c}\:=\left(−\mathrm{1},\mathrm{2},−\mathrm{3},\mathrm{4},...,\mathrm{14},−\mathrm{15}\right) \\ $$$${and}\:{a}\neq{b}\neq{c}. \\ $$$${let}\:{a}=\left(−\mathrm{1}\right)^{{p}} {p},\:{b}=\left(−\mathrm{1}\right)^{{q}} {q},\:{c}=\left(−\mathrm{1}\right)^{{r}} {r} \\ $$$$\Sigma\Sigma\Sigma{abc} \\ $$$$=\underset{{p}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\underset{{q}={p}+\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\underset{{r}={q}+\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(−\mathrm{1}\right)^{{p}+{q}+{r}} {pqr} \\ $$$$=\mathrm{4256} \\ $$
Commented by mr W last updated on 04/Nov/22
Answered by Peace last updated on 05/Nov/22
![p(x)=Σ_(n=0) ^(15) a_n x^n p(x)=Σ_(k=0) ^(15) ((p^((k)) (0))/(k!))x^k we want ((p^3 (0))/6) let ε >0 enough small such p(x)>0 ∀x∈[−ε,ε] is possible p∈R_(15) [X] Continus and p(0)=1>0 f(x)=ln(p),=Σln(1+k(−1)^k x) f′=((p′)/p)=Σ((k(−1)^k )/(1+k(−1)^k x)) f′′=((p′′)/p)−((p′^2 )/p^2 )=−Σ(k^2 /((1+k(−1)^k x)^2 )) f′′′=((p′′′)/p)−((p′p′′)/p^2 )−((2p′′p′p^2 −2p′^3 p)/p^4 )=2Σ((k^3 (−1)^k )/((1+k(−1)^k x)^3 )) p(0)=1 f′(0)=Σk(−1)^k =−8 f′′(0)=−Σk^2 =((−n(n+1)(2n+1))/6)=−40.31=−1240 f′′′(0)=2Σ(−1)^k k^3 =2.−1856=−3712 ((p′(0))/(p(0)))=−8⇒p′(0)=−8 ((p′′(0))/(p(0)))−((p′^2 (0))/(p^2 (0)))=−1240 ⇒p′′(0)=−1240+64=−1176 (3)..p′′′(0)−8.1176−(2.1176.8+1024)=−3712 p^(′′′) (0)−24.1176−1024=−3712 p′′′(0)=25536 ((p^((3)) (0))/6)=4256](Q179980.png)
$${p}\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\mathrm{15}} {\sum}}{a}_{{n}} {x}^{{n}} \\ $$$${p}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{\mathrm{15}} {\sum}}\frac{{p}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}{x}^{{k}} \:\:{we}\:{want}\:\frac{{p}^{\mathrm{3}} \left(\mathrm{0}\right)}{\mathrm{6}} \\ $$$${let}\:\epsilon\:>\mathrm{0}\:{enough}\:{small}\:{such}\:{p}\left({x}\right)>\mathrm{0}\:\forall{x}\in\left[−\epsilon,\epsilon\right] \\ $$$${is}\:{possible}\:{p}\in\mathbb{R}_{\mathrm{15}} \left[{X}\right]\:{Continus}\:{and}\:{p}\left(\mathrm{0}\right)=\mathrm{1}>\mathrm{0} \\ $$$${f}\left({x}\right)={ln}\left({p}\right),=\Sigma{ln}\left(\mathrm{1}+{k}\left(−\mathrm{1}\right)^{{k}} {x}\right) \\ $$$${f}'=\frac{{p}'}{{p}}=\Sigma\frac{{k}\left(−\mathrm{1}\right)^{{k}} }{\mathrm{1}+{k}\left(−\mathrm{1}\right)^{{k}} {x}} \\ $$$${f}''=\frac{{p}''}{{p}}−\frac{{p}'^{\mathrm{2}} }{{p}^{\mathrm{2}} }=−\Sigma\frac{{k}^{\mathrm{2}} }{\left(\mathrm{1}+{k}\left(−\mathrm{1}\right)^{{k}} {x}\right)^{\mathrm{2}} } \\ $$$${f}'''=\frac{{p}'''}{{p}}−\frac{{p}'{p}''}{{p}^{\mathrm{2}} }−\frac{\mathrm{2}{p}''{p}'{p}^{\mathrm{2}} −\mathrm{2}{p}'^{\mathrm{3}} {p}}{{p}^{\mathrm{4}} }=\mathrm{2}\Sigma\frac{{k}^{\mathrm{3}} \left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{1}+{k}\left(−\mathrm{1}\right)^{{k}} {x}\right)^{\mathrm{3}} } \\ $$$${p}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${f}'\left(\mathrm{0}\right)=\Sigma{k}\left(−\mathrm{1}\right)^{{k}} =−\mathrm{8} \\ $$$${f}''\left(\mathrm{0}\right)=−\Sigma{k}^{\mathrm{2}} =\frac{−{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}=−\mathrm{40}.\mathrm{31}=−\mathrm{1240} \\ $$$${f}'''\left(\mathrm{0}\right)=\mathrm{2}\Sigma\left(−\mathrm{1}\right)^{{k}} {k}^{\mathrm{3}} =\mathrm{2}.−\mathrm{1856}=−\mathrm{3712} \\ $$$$\frac{{p}'\left(\mathrm{0}\right)}{{p}\left(\mathrm{0}\right)}=−\mathrm{8}\Rightarrow{p}'\left(\mathrm{0}\right)=−\mathrm{8} \\ $$$$\frac{{p}''\left(\mathrm{0}\right)}{{p}\left(\mathrm{0}\right)}−\frac{{p}'^{\mathrm{2}} \left(\mathrm{0}\right)}{{p}^{\mathrm{2}} \left(\mathrm{0}\right)}=−\mathrm{1240} \\ $$$$\Rightarrow{p}''\left(\mathrm{0}\right)=−\mathrm{1240}+\mathrm{64}=−\mathrm{1176} \\ $$$$\left(\mathrm{3}\right)..{p}'''\left(\mathrm{0}\right)−\mathrm{8}.\mathrm{1176}−\left(\mathrm{2}.\mathrm{1176}.\mathrm{8}+\mathrm{1024}\right)=−\mathrm{3712} \\ $$$${p}^{'''} \left(\mathrm{0}\right)−\mathrm{24}.\mathrm{1176}−\mathrm{1024}=−\mathrm{3712} \\ $$$${p}'''\left(\mathrm{0}\right)=\mathrm{25536} \\ $$$$\frac{{p}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)}{\mathrm{6}}=\mathrm{4256} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 05/Nov/22

$${thanks}\:{alot}\:{sir}! \\ $$
Commented by mindispower last updated on 05/Nov/22
$${withe}\:{Pleasur}\:{have}\:{anice}\:{day} \\ $$
