
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 163443 by henderson last updated on 07/Jan/22

$$\mathrm{p}\:\leqslant\:\mathrm{n}\: \\ $$$$\mathrm{find}\:\:\frac{\mathrm{A}_{\mathrm{n}} ^{\mathrm{p}} }{\mathrm{A}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{p}} }. \\ $$
Commented by mr W last updated on 07/Jan/22

$${what}\:{is}\:{A}_{{n}} ? \\ $$
Commented by greg_ed last updated on 07/Jan/22

$$\mathrm{Arrangement}... \\ $$
Commented by mr W last updated on 07/Jan/22

$$\mathrm{A}_{{n}} ^{\mathrm{p}} =\mathrm{C}_{\mathrm{n}} ^{\mathrm{p}} \:{or}\:=\mathrm{P}_{\mathrm{n}} ^{\mathrm{p}} \\ $$
Commented by Ar Brandon last updated on 07/Jan/22
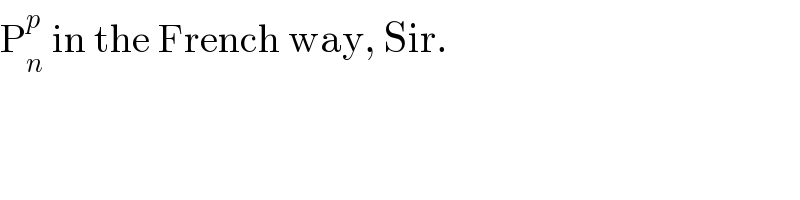
$$\mathrm{P}_{{n}} ^{{p}} \:\mathrm{in}\:\mathrm{the}\:\mathrm{French}\:\mathrm{way},\:\mathrm{Sir}. \\ $$
Commented by mr W last updated on 07/Jan/22

$${thanks}! \\ $$
Commented by mr W last updated on 07/Jan/22
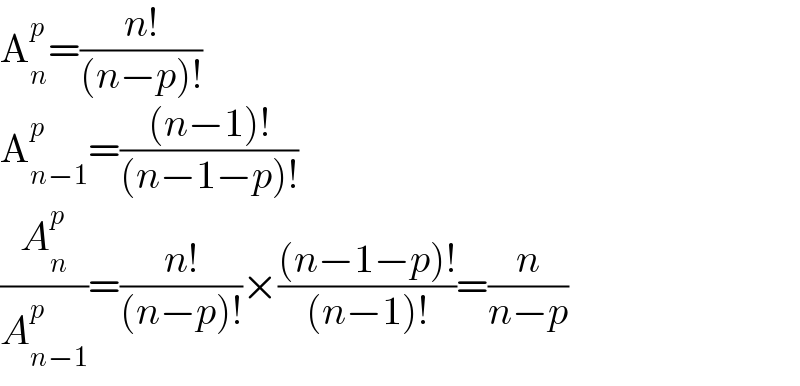
$$\mathrm{A}_{{n}} ^{{p}} =\frac{{n}!}{\left({n}−{p}\right)!} \\ $$$$\mathrm{A}_{{n}−\mathrm{1}} ^{{p}} =\frac{\left({n}−\mathrm{1}\right)!}{\left({n}−\mathrm{1}−{p}\right)!} \\ $$$$\frac{{A}_{{n}} ^{{p}} }{{A}_{{n}−\mathrm{1}} ^{{p}} }=\frac{{n}!}{\left({n}−{p}\right)!}×\frac{\left({n}−\mathrm{1}−{p}\right)!}{\left({n}−\mathrm{1}\right)!}=\frac{{n}}{{n}−{p}} \\ $$
Commented by henderson last updated on 10/Jan/22

$$\mathrm{cool}\:\:! \\ $$
