
Question Number 166839 by SANOGO last updated on 28/Feb/22
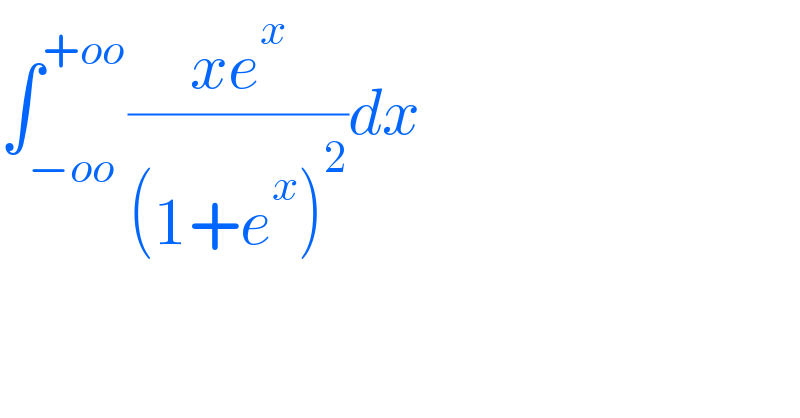
$$\int_{−{oo}} ^{+{oo}} \frac{{xe}^{{x}} }{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }{dx} \\ $$
Answered by amin96 last updated on 01/Mar/22
![e^x =t x=ln(t) (dt/dx)=t t[∞;0] ∫_0 ^∞ ((ln(t))/((1+t)^2 ))dt (1/(1+t))=x (dx/dt)=((−1)/((1+t)^2 )) x[0;1] ∫_0 ^1 ln((1/x)−1)dx=∫_0 ^1 ln(1−x)dx−∫_0 ^1 ln(x)dx= =∣_0 ^1 −(1/(1−x))−∣_0 ^1 (1/x)=−(1/0)+1−1+(1/0)=0 note ∫_0 ^1 ln(1−x)dx=∫_0 ^1 ln(x)dx](Q166841.png)
$$\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} =\boldsymbol{\mathrm{t}}\:\:\:\:\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{t}}\right)\:\:\:\:\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{dx}}}=\boldsymbol{\mathrm{t}}\:\:\:\:\boldsymbol{\mathrm{t}}\left[\infty;\mathrm{0}\right] \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{t}}\right)}{\left(\mathrm{1}+\boldsymbol{\mathrm{t}}\right)^{\mathrm{2}} }\boldsymbol{\mathrm{dt}}\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{t}}}=\boldsymbol{\mathrm{x}}\:\:\:\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{dt}}}=\frac{−\mathrm{1}}{\left(\mathrm{1}+\boldsymbol{\mathrm{t}}\right)^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{x}}\left[\mathrm{0};\mathrm{1}\right]\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{ln}}\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}−\mathrm{1}\right)\boldsymbol{\mathrm{dx}}=\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}}−\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}}= \\ $$$$=\mid_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{1}−\boldsymbol{\mathrm{x}}}−\mid_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}=−\frac{\mathrm{1}}{\mathrm{0}}+\mathrm{1}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{0}}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{note}}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}}=\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}} \\ $$
Commented by SANOGO last updated on 01/Mar/22
$${merci}\:{bien} \\ $$
