Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 196450 by cortano12 last updated on 25/Aug/23

one solution of the equation (x−a)(x−b)(x−c)(x−d) = 9 is x=2. If a,b,c,d are different integers then a+b+c+d =?

$$\mathrm{one}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\:\left(\mathrm{x}−\mathrm{a}\right)\left(\mathrm{x}−\mathrm{b}\right)\left(\mathrm{x}−\mathrm{c}\right)\left(\mathrm{x}−\mathrm{d}\right)\:=\:\mathrm{9}\: \\ $$$$\:\mathrm{is}\:\mathrm{x}=\mathrm{2}.\:\mathrm{If}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\mathrm{are}\:\mathrm{different}\: \\ $$$$\:\mathrm{integers}\:\mathrm{then}\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\:=?\: \\ $$

Answered by Rasheed.Sindhi last updated on 25/Aug/23

(x−a)(x−b)(x−c)(x−d) = 9 x=2 x=2 (2−a)(2−b)(2−c)(2−d)=9 a,b,c,d are different integers ⇒2−a,2−b,2−c,2−d are different integers. • 9=1×−1×3×−3 [Order no matters] 2−a=1⇒a=1 2−b=−1⇒b=3 2−c=3⇒c=−1 2−d=−3⇒d=5 a+b+c+d=8✓

$$\left(\mathrm{x}−\mathrm{a}\right)\left(\mathrm{x}−\mathrm{b}\right)\left(\mathrm{x}−\mathrm{c}\right)\left(\mathrm{x}−\mathrm{d}\right)\:=\:\mathrm{9} \\ $$$$\mathrm{x}=\mathrm{2}\: \\ $$$$\mathrm{x}=\mathrm{2} \\ $$$$\left(\mathrm{2}−\mathrm{a}\right)\left(\mathrm{2}−\mathrm{b}\right)\left(\mathrm{2}−\mathrm{c}\right)\left(\mathrm{2}−\mathrm{d}\right)=\mathrm{9} \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\mathrm{are}\:\mathrm{different}\:\mathrm{integers} \\ $$$$\Rightarrow\mathrm{2}−\mathrm{a},\mathrm{2}−\mathrm{b},\mathrm{2}−\mathrm{c},\mathrm{2}−\mathrm{d}\:\mathrm{are}\:\mathrm{different}\:\mathrm{integers}. \\ $$$$\: \\ $$$$\bullet\:\mathrm{9}=\mathrm{1}×−\mathrm{1}×\mathrm{3}×−\mathrm{3}\:\left[{Order}\:{no}\:{matters}\right] \\ $$$$\mathrm{2}−\mathrm{a}=\mathrm{1}\Rightarrow\mathrm{a}=\mathrm{1} \\ $$$$\mathrm{2}−\mathrm{b}=−\mathrm{1}\Rightarrow\mathrm{b}=\mathrm{3} \\ $$$$\mathrm{2}−\mathrm{c}=\mathrm{3}\Rightarrow\mathrm{c}=−\mathrm{1} \\ $$$$\mathrm{2}−\mathrm{d}=−\mathrm{3}\Rightarrow\mathrm{d}=\mathrm{5} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=\mathrm{8}\checkmark \\ $$

Answered by MM42 last updated on 25/Aug/23

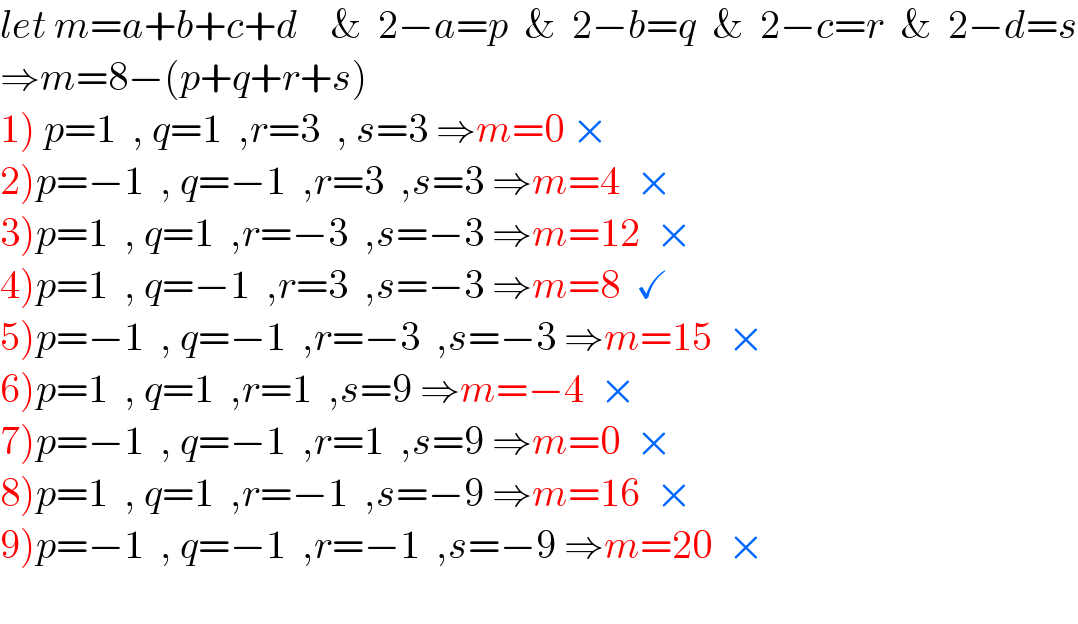
let m=a+b+c+d & 2−a=p & 2−b=q & 2−c=r & 2−d=s ⇒m=8−(p+q+r+s) 1) p=1 , q=1 ,r=3 , s=3 ⇒m=0 × 2)p=−1 , q=−1 ,r=3 ,s=3 ⇒m=4 × 3)p=1 , q=1 ,r=−3 ,s=−3 ⇒m=12 × 4)p=1 , q=−1 ,r=3 ,s=−3 ⇒m=8 ✓ 5)p=−1 , q=−1 ,r=−3 ,s=−3 ⇒m=15 × 6)p=1 , q=1 ,r=1 ,s=9 ⇒m=−4 × 7)p=−1 , q=−1 ,r=1 ,s=9 ⇒m=0 × 8)p=1 , q=1 ,r=−1 ,s=−9 ⇒m=16 × 9)p=−1 , q=−1 ,r=−1 ,s=−9 ⇒m=20 ×

$${let}\:{m}={a}+{b}+{c}+{d}\:\:\:\:\&\:\:\mathrm{2}−{a}={p}\:\:\&\:\:\mathrm{2}−{b}={q}\:\:\&\:\:\mathrm{2}−{c}={r}\:\:\&\:\:\mathrm{2}−{d}={s} \\ $$$$\Rightarrow{m}=\mathrm{8}−\left({p}+{q}+{r}+{s}\right) \\ $$$$\left.\mathrm{1}\right)\:{p}=\mathrm{1}\:\:,\:{q}=\mathrm{1}\:\:,{r}=\mathrm{3}\:\:,\:{s}=\mathrm{3}\:\Rightarrow{m}=\mathrm{0}\:× \\ $$$$\left.\mathrm{2}\right){p}=−\mathrm{1}\:\:,\:{q}=−\mathrm{1}\:\:,{r}=\mathrm{3}\:\:,{s}=\mathrm{3}\:\Rightarrow{m}=\mathrm{4}\:\:× \\ $$$$\left.\mathrm{3}\right){p}=\mathrm{1}\:\:,\:{q}=\mathrm{1}\:\:,{r}=−\mathrm{3}\:\:,{s}=−\mathrm{3}\:\Rightarrow{m}=\mathrm{12}\:\:× \\ $$$$\left.\mathrm{4}\right){p}=\mathrm{1}\:\:,\:{q}=−\mathrm{1}\:\:,{r}=\mathrm{3}\:\:,{s}=−\mathrm{3}\:\Rightarrow{m}=\mathrm{8}\:\:\checkmark \\ $$$$\left.\mathrm{5}\right){p}=−\mathrm{1}\:\:,\:{q}=−\mathrm{1}\:\:,{r}=−\mathrm{3}\:\:,{s}=−\mathrm{3}\:\Rightarrow{m}=\mathrm{15}\:\:× \\ $$$$\left.\mathrm{6}\right){p}=\mathrm{1}\:\:,\:{q}=\mathrm{1}\:\:,{r}=\mathrm{1}\:\:,{s}=\mathrm{9}\:\Rightarrow{m}=−\mathrm{4}\:\:× \\ $$$$\left.\mathrm{7}\right){p}=−\mathrm{1}\:\:,\:{q}=−\mathrm{1}\:\:,{r}=\mathrm{1}\:\:,{s}=\mathrm{9}\:\Rightarrow{m}=\mathrm{0}\:\:× \\ $$$$\left.\mathrm{8}\right){p}=\mathrm{1}\:\:,\:{q}=\mathrm{1}\:\:,{r}=−\mathrm{1}\:\:,{s}=−\mathrm{9}\:\Rightarrow{m}=\mathrm{16}\:\:× \\ $$$$\left.\mathrm{9}\right){p}=−\mathrm{1}\:\:,\:{q}=−\mathrm{1}\:\:,{r}=−\mathrm{1}\:\:,{s}=−\mathrm{9}\:\Rightarrow{m}=\mathrm{20}\:\:× \\ $$$$ \\ $$

Answered by mr W last updated on 25/Aug/23

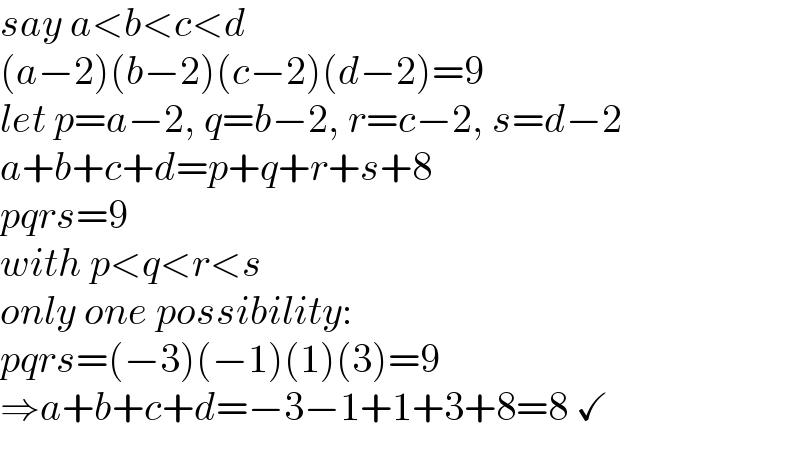
say a<b<c<d (a−2)(b−2)(c−2)(d−2)=9 let p=a−2, q=b−2, r=c−2, s=d−2 a+b+c+d=p+q+r+s+8 pqrs=9 with p<q<r<s only one possibility: pqrs=(−3)(−1)(1)(3)=9 ⇒a+b+c+d=−3−1+1+3+8=8 ✓

$${say}\:{a}<{b}<{c}<{d} \\ $$$$\left({a}−\mathrm{2}\right)\left({b}−\mathrm{2}\right)\left({c}−\mathrm{2}\right)\left({d}−\mathrm{2}\right)=\mathrm{9} \\ $$$${let}\:{p}={a}−\mathrm{2},\:{q}={b}−\mathrm{2},\:{r}={c}−\mathrm{2},\:{s}={d}−\mathrm{2} \\ $$$${a}+{b}+{c}+{d}={p}+{q}+{r}+{s}+\mathrm{8} \\ $$$${pqrs}=\mathrm{9} \\ $$$${with}\:{p}<{q}<{r}<{s} \\ $$$${only}\:{one}\:{possibility}: \\ $$$${pqrs}=\left(−\mathrm{3}\right)\left(−\mathrm{1}\right)\left(\mathrm{1}\right)\left(\mathrm{3}\right)=\mathrm{9} \\ $$$$\Rightarrow{a}+{b}+{c}+{d}=−\mathrm{3}−\mathrm{1}+\mathrm{1}+\mathrm{3}+\mathrm{8}=\mathrm{8}\:\checkmark \\ $$

Commented by MM42 last updated on 25/Aug/23

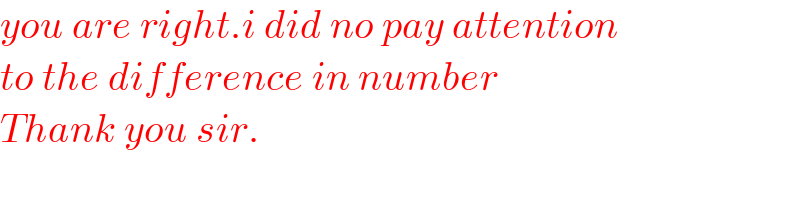
you are right.i did no pay attention to the difference in number Thank you sir.

$${you}\:{are}\:{right}.{i}\:{did}\:{no}\:{pay}\:{attention}\: \\ $$$${to}\:{the}\:{difference}\:{in}\:{number} \\ $$$${Thank}\:{you}\:{sir}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com