
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 149532 by ArielVyny last updated on 06/Aug/21
![on realise une suite infinie d′epreuves independantes.chaque epreuve resulte en un succes avec la probabilite p∈]0;1[ ou un echec avec la probabilite q=1−p.soit A_n l′evement “obenir au moins un succes au cours des premieres epreuves.” determiner P(A_n )](Q149532.png)
$${on}\:{realise}\:{une}\:{suite}\:{infinie}\:{d}'{epreuves} \\ $$$${independantes}.{chaque}\:{epreuve}\:{resulte}\:{en} \\ $$$$\left.{un}\:{succes}\:{avec}\:{la}\:{probabilite}\:{p}\in\right]\mathrm{0};\mathrm{1}\left[\:{ou}\:{un}\right. \\ $$$${echec}\:{avec}\:{la}\:{probabilite}\:{q}=\mathrm{1}−{p}.{soit}\:{A}_{{n}} \\ $$$${l}'{evement}\:``{obenir}\:{au}\:{moins}\:{un}\:{succes}\:{au} \\ $$$${cours}\:{des}\:{premieres}\:{epreuves}.''\:{determiner} \\ $$$${P}\left({A}_{{n}} \right) \\ $$
Answered by Olaf_Thorendsen last updated on 06/Aug/21

$$\mathrm{La}\:\mathrm{succession}\:\mathrm{de}\:{n}\:\mathrm{epreuves}\:\mathrm{de} \\ $$$$\mathrm{Bernoulli}\:\mathrm{est}\:\mathrm{une}\:\mathrm{loi}\:\mathrm{binomiale}\:\mathscr{B}\left({n},{p}\right) \\ $$$$\mathrm{P}\left(\mathrm{X}={k}\right)\:=\:\mathrm{C}_{{k}} ^{{n}} {p}^{{k}} {q}^{{n}−{k}} \\ $$$$\mathrm{L}'\mathrm{evenement}\:``\mathrm{au}\:\mathrm{moins}\:\mathrm{un}\:\mathrm{succes}''\:\mathrm{est} \\ $$$$\mathrm{le}\:\mathrm{complementaire}\:\mathrm{de}\:\mathrm{l}'\mathrm{evenement} \\ $$$$``\mathrm{Aucun}\:\mathrm{succes}''\:\mathrm{et}\:\mathrm{donc}\:: \\ $$$$\mathrm{P}\left(\mathrm{X}\geqslant\mathrm{1}\right)\:=\:\mathrm{1}−\mathrm{P}\left(\mathrm{X}=\mathrm{0}\right)\:=\:\mathrm{1}−\mathrm{C}_{\mathrm{0}} ^{{n}} {p}^{{n}} {q}^{{n}−{k}} \\ $$$$=\:\mathrm{1}−{p}^{{n}} {q}^{{n}−{k}} \\ $$
Commented by ArielVyny last updated on 06/Aug/21
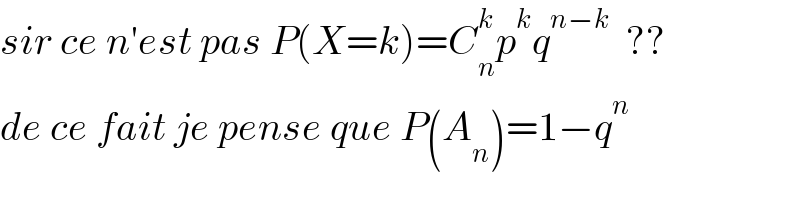
$${sir}\:{ce}\:{n}'{est}\:{pas}\:{P}\left({X}={k}\right)={C}_{{n}} ^{{k}} {p}^{{k}} {q}^{{n}−{k}} \:\:?? \\ $$$${de}\:{ce}\:{fait}\:{je}\:{pense}\:{que}\:{P}\left({A}_{{n}} \right)=\mathrm{1}−{q}^{{n}} \\ $$
