Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7610 by Tawakalitu. last updated on 06/Sep/16

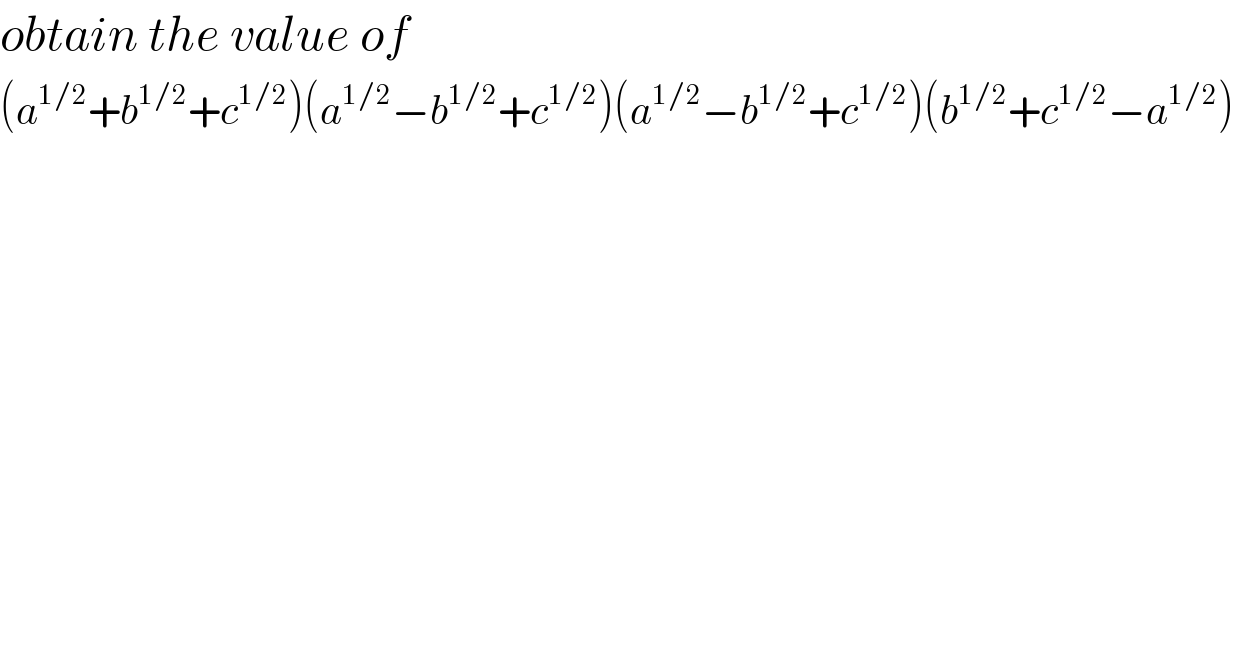
obtain the value of (a^(1/2) +b^(1/2) +c^(1/2) )(a^(1/2) −b^(1/2) +c^(1/2) )(a^(1/2) −b^(1/2) +c^(1/2) )(b^(1/2) +c^(1/2) −a^(1/2) )

$${obtain}\:{the}\:{value}\:{of}\: \\ $$$$\left({a}^{\mathrm{1}/\mathrm{2}} +{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({a}^{\mathrm{1}/\mathrm{2}} −{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({a}^{\mathrm{1}/\mathrm{2}} −{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} −{a}^{\mathrm{1}/\mathrm{2}} \right)\: \\ $$

Commented by Rasheed Soomro last updated on 06/Sep/16

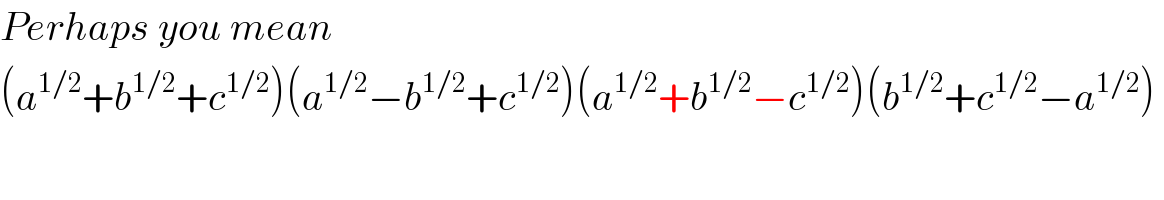
Perhaps you mean (a^(1/2) +b^(1/2) +c^(1/2) )(a^(1/2) −b^(1/2) +c^(1/2) )(a^(1/2) +b^(1/2) −c^(1/2) )(b^(1/2) +c^(1/2) −a^(1/2) )

$${Perhaps}\:{you}\:{mean} \\ $$$$\left({a}^{\mathrm{1}/\mathrm{2}} +{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({a}^{\mathrm{1}/\mathrm{2}} −{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({a}^{\mathrm{1}/\mathrm{2}} +{b}^{\mathrm{1}/\mathrm{2}} −{c}^{\mathrm{1}/\mathrm{2}} \right)\left({b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} −{a}^{\mathrm{1}/\mathrm{2}} \right)\: \\ $$

Commented by Tawakalitu. last updated on 06/Sep/16

Alright sir.. thank you. is like that.

$${Alright}\:{sir}..\:{thank}\:{you}.\:{is}\:{like}\:{that}. \\ $$

Answered by Rasheed Soomro last updated on 06/Sep/16

(a^(1/2) +b^(1/2) +c^(1/2) )(a^(1/2) −b^(1/2) +c^(1/2) )(a^(1/2) +b^(1/2) −c^(1/2) )(b^(1/2) +c^(1/2) −a^(1/2) ) Let a^(1/2) =p , b^(1/2) =q , c^(1/2) =r (p+q+r)(p−q+r)(p+q−r)(−p+q+r) {(p+r)+q}{(p+r)−q}{q+(p−r)}{q−(p−r)} {(p+r)^2 −q^2 }{q^2 −(p−r)^2 } (p^2 +2pr+r^2 −q^2 )(q^2 −p^2 +2pr−r^2 ) {2pr+(p^2 −q^2 +r^2 )}{2pr−(p^2 −q^2 +r^2 )} (2pr)^2 −(p^2 −q^2 +r^2 )^2 4p^2 r^2 −(p^4 +q^4 +r^4 −2p^2 q^2 −2q^2 r^2 +2p^2 r^2 ) 2p^2 r^2 −p^4 −q^4 −r^4 +2p^2 q^2 +2q^2 r^2 p=a^(1/2) ⇒p^2 =a⇒p^4 =a^2 q=b^(1/2) ⇒q^2 =b⇒q^4 =b^2 r=c^(1/2) ⇒r^2 =c⇒r^4 =c^2 2p^2 r^2 −p^4 −q^4 −r^4 +2p^2 q^2 +2q^2 r^2 =2ac−a^2 −b^2 −c^2 +2ab+2bc =−(a^2 +b^2 +c^2 −2ab−2bc−2ca)

$$\left({a}^{\mathrm{1}/\mathrm{2}} +{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({a}^{\mathrm{1}/\mathrm{2}} −{b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} \right)\left({a}^{\mathrm{1}/\mathrm{2}} +{b}^{\mathrm{1}/\mathrm{2}} −{c}^{\mathrm{1}/\mathrm{2}} \right)\left({b}^{\mathrm{1}/\mathrm{2}} +{c}^{\mathrm{1}/\mathrm{2}} −{a}^{\mathrm{1}/\mathrm{2}} \right)\: \\ $$$${Let}\:\:{a}^{\mathrm{1}/\mathrm{2}} ={p}\:,\:{b}^{\mathrm{1}/\mathrm{2}} ={q}\:,\:{c}^{\mathrm{1}/\mathrm{2}} ={r} \\ $$$$\left({p}+{q}+{r}\right)\left({p}−{q}+{r}\right)\left({p}+{q}−{r}\right)\left(−{p}+{q}+{r}\right) \\ $$$$\left\{\left({p}+{r}\right)+{q}\right\}\left\{\left({p}+{r}\right)−{q}\right\}\left\{{q}+\left({p}−{r}\right)\right\}\left\{{q}−\left({p}−{r}\right)\right\} \\ $$$$\left\{\left({p}+{r}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right\}\left\{{q}^{\mathrm{2}} −\left({p}−{r}\right)^{\mathrm{2}} \right\} \\ $$$$\left({p}^{\mathrm{2}} +\mathrm{2}{pr}+{r}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} −{p}^{\mathrm{2}} +\mathrm{2}{pr}−{r}^{\mathrm{2}} \right) \\ $$$$\left\{\mathrm{2}{pr}+\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\right\}\left\{\mathrm{2}{pr}−\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\right\} \\ $$$$\left(\mathrm{2}{pr}\right)^{\mathrm{2}} −\left({p}^{\mathrm{2}} −{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{4}{p}^{\mathrm{2}} {r}^{\mathrm{2}} −\left({p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} −\mathrm{2}{p}^{\mathrm{2}} {q}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} {r}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{2}} {r}^{\mathrm{2}} \right) \\ $$$$\mathrm{2}{p}^{\mathrm{2}} {r}^{\mathrm{2}} −{p}^{\mathrm{4}} −{q}^{\mathrm{4}} −{r}^{\mathrm{4}} +\mathrm{2}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{2}{q}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$${p}={a}^{\mathrm{1}/\mathrm{2}} \Rightarrow{p}^{\mathrm{2}} ={a}\Rightarrow{p}^{\mathrm{4}} ={a}^{\mathrm{2}} \\ $$$${q}={b}^{\mathrm{1}/\mathrm{2}} \Rightarrow{q}^{\mathrm{2}} ={b}\Rightarrow{q}^{\mathrm{4}} ={b}^{\mathrm{2}} \\ $$$${r}={c}^{\mathrm{1}/\mathrm{2}} \Rightarrow{r}^{\mathrm{2}} ={c}\Rightarrow{r}^{\mathrm{4}} ={c}^{\mathrm{2}} \\ $$$$\mathrm{2}{p}^{\mathrm{2}} {r}^{\mathrm{2}} −{p}^{\mathrm{4}} −{q}^{\mathrm{4}} −{r}^{\mathrm{4}} +\mathrm{2}{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{2}{q}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{ac}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{c}^{\mathrm{2}} +\mathrm{2}{ab}+\mathrm{2bc} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ab}−\mathrm{2}{bc}−\mathrm{2}{ca}\right) \\ $$

Commented by Tawakalitu. last updated on 06/Sep/16

wow, thank you sir. God bless you

$${wow},\:{thank}\:{you}\:{sir}.\:{God}\:{bless}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com