
Question Number 186223 by SANOGO last updated on 02/Feb/23
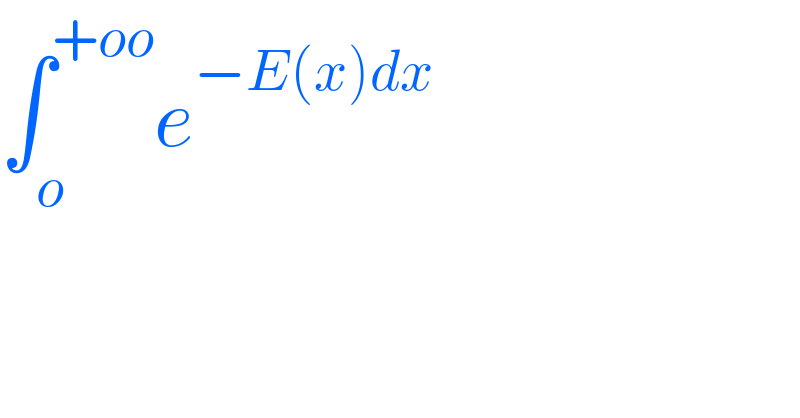
$$\int_{{o}} ^{+{oo}} {e}^{−{E}\left({x}\right){dx}} \\ $$
Answered by Mathspace last updated on 02/Feb/23
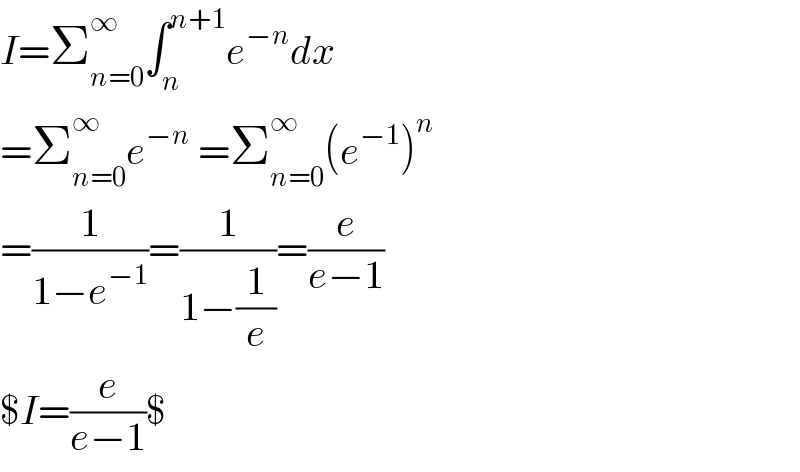
$${I}=\sum_{{n}=\mathrm{0}} ^{\infty} \int_{{n}} ^{{n}+\mathrm{1}} {e}^{−{n}} {dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} {e}^{−{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left({e}^{−\mathrm{1}} \right)^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{e}^{−\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{e}}}=\frac{{e}}{{e}−\mathrm{1}} \\ $$$$\${I}=\frac{{e}}{{e}−\mathrm{1}}\$ \\ $$
Commented by SANOGO last updated on 02/Feb/23
$${merci}\:{bien} \\ $$
Commented by Mathspace last updated on 03/Feb/23

$${you}\:{are}\:{welcome} \\ $$
