
Question Number 93911 by i jagooll last updated on 16/May/20
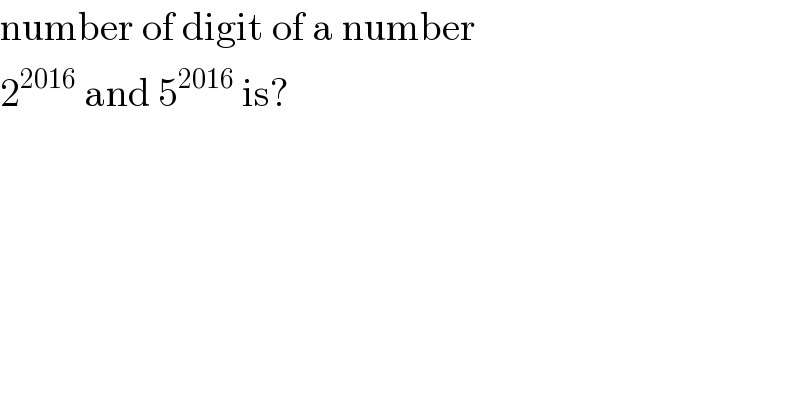
$$\mathrm{number}\:\mathrm{of}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{a}\:\mathrm{number}\: \\ $$$$\mathrm{2}^{\mathrm{2016}} \:\mathrm{and}\:\mathrm{5}^{\mathrm{2016}} \:\mathrm{is}? \\ $$
Commented by PRITHWISH SEN 2 last updated on 16/May/20
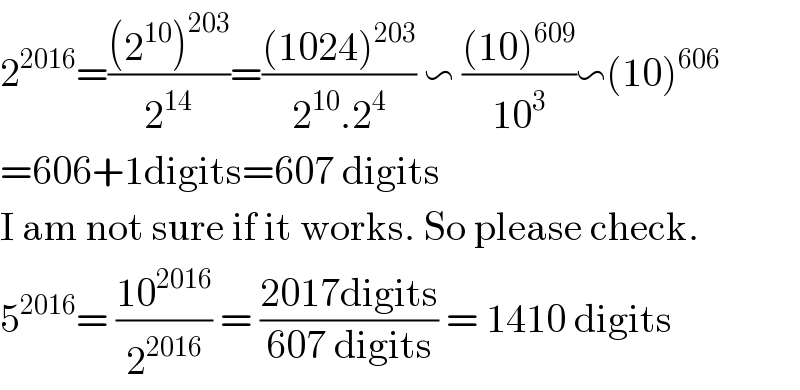
$$\mathrm{2}^{\mathrm{2016}} =\frac{\left(\mathrm{2}^{\mathrm{10}} \right)^{\mathrm{203}} }{\mathrm{2}^{\mathrm{14}} }=\frac{\left(\mathrm{1024}\right)^{\mathrm{203}} }{\mathrm{2}^{\mathrm{10}} .\mathrm{2}^{\mathrm{4}} }\:\backsim\:\frac{\left(\mathrm{10}\right)^{\mathrm{609}} }{\mathrm{10}^{\mathrm{3}} }\backsim\left(\mathrm{10}\right)^{\mathrm{606}} \\ $$$$=\mathrm{606}+\mathrm{1digits}=\mathrm{607}\:\mathrm{digits} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{it}\:\mathrm{works}.\:\mathrm{So}\:\mathrm{please}\:\mathrm{check}. \\ $$$$\mathrm{5}^{\mathrm{2016}} =\:\frac{\mathrm{10}^{\mathrm{2016}} }{\mathrm{2}^{\mathrm{2016}} }\:=\:\frac{\mathrm{2017digits}}{\mathrm{607}\:\mathrm{digits}}\:=\:\mathrm{1410}\:\mathrm{digits} \\ $$
Commented by i jagooll last updated on 16/May/20
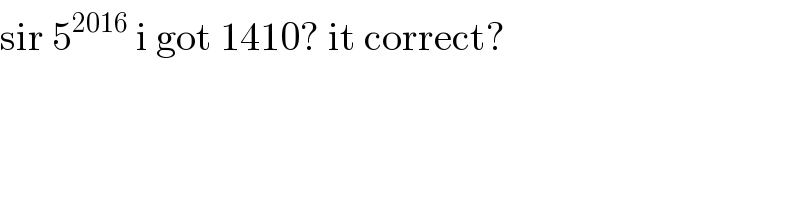
$$\mathrm{sir}\:\mathrm{5}^{\mathrm{2016}} \:\mathrm{i}\:\mathrm{got}\:\mathrm{1410}?\:\mathrm{it}\:\mathrm{correct}? \\ $$
Commented by Tony Lin last updated on 16/May/20
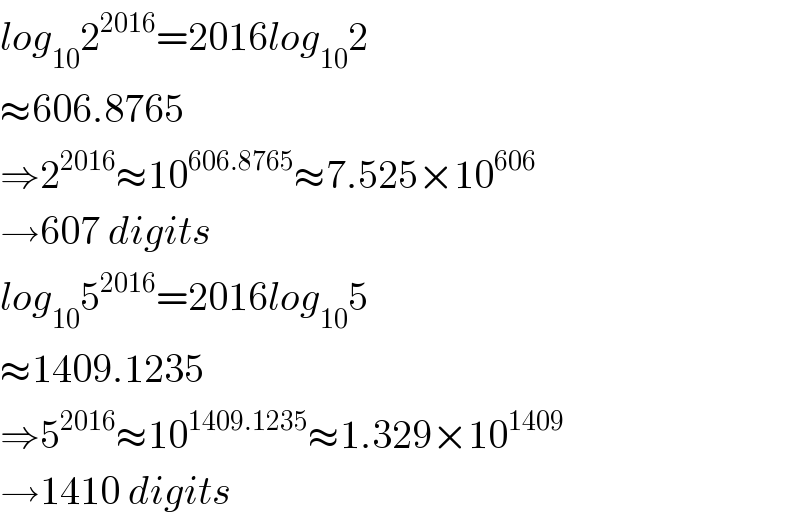
$${log}_{\mathrm{10}} \mathrm{2}^{\mathrm{2016}} =\mathrm{2016}{log}_{\mathrm{10}} \mathrm{2} \\ $$$$\approx\mathrm{606}.\mathrm{8765} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{2016}} \approx\mathrm{10}^{\mathrm{606}.\mathrm{8765}} \approx\mathrm{7}.\mathrm{525}×\mathrm{10}^{\mathrm{606}} \\ $$$$\rightarrow\mathrm{607}\:{digits} \\ $$$${log}_{\mathrm{10}} \mathrm{5}^{\mathrm{2016}} =\mathrm{2016}{log}_{\mathrm{10}} \mathrm{5} \\ $$$$\approx\mathrm{1409}.\mathrm{1235} \\ $$$$\Rightarrow\mathrm{5}^{\mathrm{2016}} \approx\mathrm{10}^{\mathrm{1409}.\mathrm{1235}} \approx\mathrm{1}.\mathrm{329}×\mathrm{10}^{\mathrm{1409}} \\ $$$$\rightarrow\mathrm{1410}\:{digits} \\ $$
Commented by PRITHWISH SEN 2 last updated on 16/May/20
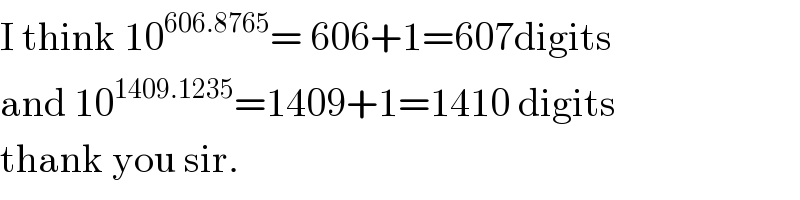
$$\mathrm{I}\:\mathrm{think}\:\mathrm{10}^{\mathrm{606}.\mathrm{8765}} =\:\mathrm{606}+\mathrm{1}=\mathrm{607digits} \\ $$$$\mathrm{and}\:\mathrm{10}^{\mathrm{1409}.\mathrm{1235}} =\mathrm{1409}+\mathrm{1}=\mathrm{1410}\:\mathrm{digits} \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by i jagooll last updated on 16/May/20
what if students don't memorize grades from log base (10) 2 and log base (10) 5 sir?
Commented by i jagooll last updated on 16/May/20
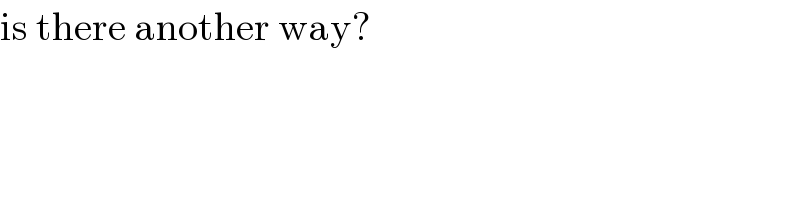
$$\mathrm{is}\:\mathrm{there}\:\mathrm{another}\:\mathrm{way}? \\ $$
Commented by Tony Lin last updated on 16/May/20
![actually log5=1−log2 just remember log2≈0.3010 log3≈0.4771 log7≈0.8451 in senior high school Teachers asked us to remember these three common values, which is easy to evalute a^(±b) if b is a large number And sometimes it would give you the value in the test,so there′s no worry about it in university Calculators are allowed in some courses And logarithm is not the main topic of the test But One method to evaluate logarithm I came up with is using Taylor series log2=((ln2)/(ln10)) We know that ln(1+x)=x−(x^2 /2)+(x^3 /3)−(x^4 /4)+∙∙∙ for −1<x≤1 plug 1 in ⇒ln2=1−(1/2)+(1/3)−(1/4)+∙∙∙≈0.693147 We cannot plug 9 in the Mercator series because −1<x≤1 but we can use ln(((1+x)/(1−x))) =ln(1+x)−ln(1−x) plug (9/(11)) in so ln10 =[(9/(11))−((((9/(11)))^2 )/2)+((((9/(11)))^3 )/3)−((((9/(11)))^4 )/4)+∙∙∙] +[(9/(11))+((((9/(11)))^2 )/2)+((((9/(11)))^3 )/3)+((((9/(11)))^4 )/4)+∙∙∙] =2×[(9/(11))+((((9/(11)))^3 )/3)+((((9/(11)))^5 )/5)+∙∙∙] =2×((9/(11))/(1−((9/(11)))^2 ))(1+(1/3)+(1/5)+∙∙∙) ≈2.302585 ∴log2=((ln2)/(ln10))≈0.3010](Q93942.png)
$${actually} \\ $$$${log}\mathrm{5}=\mathrm{1}−{log}\mathrm{2} \\ $$$${just}\:{remember}\: \\ $$$${log}\mathrm{2}\approx\mathrm{0}.\mathrm{3010} \\ $$$${log}\mathrm{3}\approx\mathrm{0}.\mathrm{4771} \\ $$$${log}\mathrm{7}\approx\mathrm{0}.\mathrm{8451} \\ $$$${in}\:{senior}\:{high}\:{school} \\ $$$${Teachers}\:{asked}\:{us}\:{to}\:{remember}\:{these} \\ $$$${three}\:{common}\:{values},\:{which}\:{is}\:{easy} \\ $$$${to}\:{evalute}\:{a}^{\pm{b}} \:{if}\:{b}\:{is}\:{a}\:{large}\:{number} \\ $$$${And}\:{sometimes}\:{it}\:{would}\:{give}\:{you}\:{the} \\ $$$${value}\:{in}\:{the}\:{test},{so}\:{there}'{s}\:{no}\:{worry} \\ $$$${about}\:{it} \\ $$$${in}\:{university} \\ $$$${Calculators}\:{are}\:{allowed}\:{in}\:{some}\:{courses} \\ $$$${And}\:{logarithm}\:{is}\:{not}\:{the}\:{main}\:{topic} \\ $$$${of}\:{the}\:{test} \\ $$$$\:\boldsymbol{{But}} \\ $$$${One}\:{method}\:{to}\:{evaluate}\:{logarithm} \\ $$$${I}\:{came}\:{up}\:{with}\:{is}\:{using}\:{Taylor}\:{series} \\ $$$${log}\mathrm{2}=\frac{{ln}\mathrm{2}}{{ln}\mathrm{10}} \\ $$$${We}\:{know}\:{that}\: \\ $$$${ln}\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+\centerdot\centerdot\centerdot \\ $$$${for}\:−\mathrm{1}<{x}\leqslant\mathrm{1} \\ $$$${plug}\:\mathrm{1}\:{in}\: \\ $$$$\Rightarrow{ln}\mathrm{2}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\centerdot\centerdot\centerdot\approx\mathrm{0}.\mathrm{693147} \\ $$$${We}\:{cannot}\:{plug}\:\mathrm{9}\:{in}\:{the}\:{Mercator}\:{series} \\ $$$${because}\:−\mathrm{1}<{x}\leqslant\mathrm{1} \\ $$$${but}\:{we}\:{can}\:{use}\: \\ $$$${ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right) \\ $$$$={ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right) \\ $$$${plug}\:\frac{\mathrm{9}}{\mathrm{11}}\:{in} \\ $$$${so}\:{ln}\mathrm{10} \\ $$$$=\left[\frac{\mathrm{9}}{\mathrm{11}}−\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{3}} }{\mathrm{3}}−\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{4}} }{\mathrm{4}}+\centerdot\centerdot\centerdot\right] \\ $$$$+\left[\frac{\mathrm{9}}{\mathrm{11}}+\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{3}} }{\mathrm{3}}+\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{4}} }{\mathrm{4}}+\centerdot\centerdot\centerdot\right] \\ $$$$=\mathrm{2}×\left[\frac{\mathrm{9}}{\mathrm{11}}+\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{3}} }{\mathrm{3}}+\frac{\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{5}} }{\mathrm{5}}+\centerdot\centerdot\centerdot\right] \\ $$$$=\mathrm{2}×\frac{\frac{\mathrm{9}}{\mathrm{11}}}{\mathrm{1}−\left(\frac{\mathrm{9}}{\mathrm{11}}\right)^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\centerdot\centerdot\centerdot\right) \\ $$$$\approx\mathrm{2}.\mathrm{302585} \\ $$$$\therefore{log}\mathrm{2}=\frac{{ln}\mathrm{2}}{{ln}\mathrm{10}}\approx\mathrm{0}.\mathrm{3010} \\ $$
Commented by i jagooll last updated on 16/May/20

$$\mathrm{ok}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$
