Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 139217 by mnjuly1970 last updated on 24/Apr/21

..... nice .... .... math.... prove that: 𝛗=∫_0 ^( (Ο€/2)) ((ln(1+sin(x).cos(x)))/(tan(x)))dx=((5Ο€^2 )/(72))

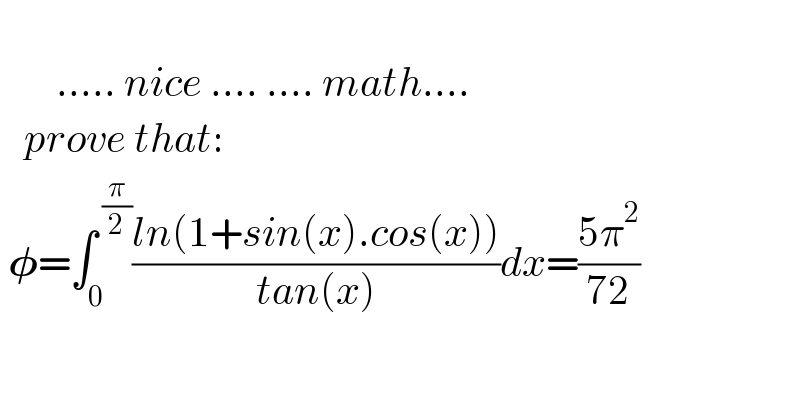
$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:.....\:{nice}\:....\:....\:{math}.... \\ $$$$\:\:\:{prove}\:{that}: \\ $$$$\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}+{sin}\left({x}\right).{cos}\left({x}\right)\right)}{{tan}\left({x}\right)}{dx}=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{72}} \\ $$

Commented by liki last updated on 24/Apr/21

Commented by liki last updated on 24/Apr/21

..help pls

$$..\mathrm{help}\:\mathrm{pls} \\ $$

Commented by mr W last updated on 24/Apr/21

to liki: please donβ€²t insert your question into the threads of other people for other questions! just open a new thread for your own question! if you donβ€²t know how, just read the ForumHelp!

$${to}\:{liki}: \\ $$$${please}\:{don}'{t}\:{insert}\:{your}\:{question}\:{into} \\ $$$${the}\:{threads}\:{of}\:{other}\:{people}\:{for}\:{other} \\ $$$${questions}!\:{just}\:{open}\:{a}\:{new}\:{thread}\:{for} \\ $$$${your}\:{own}\:{question}!\:{if}\:{you}\:{don}'{t}\:{know} \\ $$$${how},\:{just}\:{read}\:{the}\:{ForumHelp}! \\ $$

Answered by qaz last updated on 24/Apr/21

Ο†=∫_0 ^(Ο€/2) ((ln(1+sin xcos x))/(tan x))dx =∫_0 ^(Ο€/2) ((ln(1+((tan x)/(1+tan^2 x))))/(tan x))dx =∫_0 ^(Ο€/2) ((ln(1+tan x+tan^2 x)βˆ’ln(1+tan^2 x))/(tan x))dx =∫_0 ^∞ ((ln(1+x+x^2 )βˆ’ln(1+x^2 ))/(x(1+x^2 )))dx =∫_0 ^1 ((ln(1+x+x^2 )βˆ’ln(1+x^2 ))/(x(1+x^2 )))dx+∫_1 ^∞ ((ln(1+x+x^2 )βˆ’ln(1+x^2 ))/((1/x)(1+(1/x^2 ))))(βˆ’(1/x^2 ))dx =∫_0 ^1 ((ln(1+x+x^2 )βˆ’ln(1+x^2 ))/(x(1+x^2 )))dx+∫_0 ^1 ((ln(1+x+x^2 )βˆ’ln(1+x^2 ))/(1+x^2 ))xdx =∫_0 ^1 ((ln(1+x+x^2 )βˆ’ln(1+x^2 ))/x)dx =∫_0 ^1 ((ln(1βˆ’x^3 )βˆ’ln(1βˆ’x))/x)dxβˆ’(1/2)Ξ·(2) =βˆ’Ξ£_(n=1) ^∞ ∫_0 ^1 (x^(3nβˆ’1) /n)dx+(Ο€^2 /6)βˆ’(Ο€^2 /(24)) =βˆ’Ξ£_(n=1) ^∞ (1/(3n^2 ))+(Ο€^2 /8) =βˆ’(Ο€^2 /(18))+(Ο€^2 /8) =((5Ο€^2 )/(72))

$$\phi=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\left(\mathrm{1}+\mathrm{sin}\:{x}\mathrm{cos}\:{x}\right)}{\mathrm{tan}\:{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\left(\mathrm{1}+\frac{\mathrm{tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}}\right)}{\mathrm{tan}\:{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\left(\mathrm{1}+\mathrm{tan}\:{x}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)βˆ’{ln}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)}{\mathrm{tan}\:{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)βˆ’{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)βˆ’{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)βˆ’{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\frac{\mathrm{1}}{{x}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}\left(βˆ’\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)βˆ’{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)βˆ’{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)βˆ’{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}βˆ’{x}^{\mathrm{3}} \right)βˆ’{ln}\left(\mathrm{1}βˆ’{x}\right)}{{x}}{dx}βˆ’\frac{\mathrm{1}}{\mathrm{2}}\eta\left(\mathrm{2}\right) \\ $$$$=βˆ’\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}{n}βˆ’\mathrm{1}} }{{n}}{dx}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$$$=βˆ’\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} }+\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$=βˆ’\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{72}} \\ $$

Commented by mnjuly1970 last updated on 24/Apr/21

great, thanks alot master...

$$\:\:{great},\:{thanks}\:{alot}\:{master}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com