
Question Number 140789 by mnjuly1970 last updated on 12/May/21
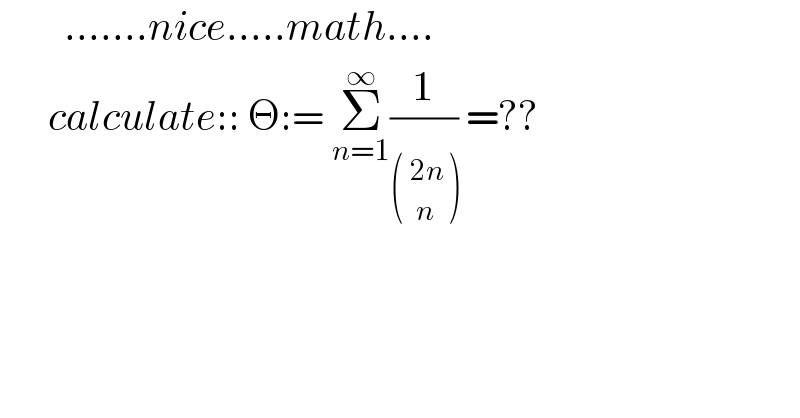
$$\:\:\:\:\:\:\:\:.......{nice}.....{math}.... \\ $$$$\:\:\:\:\:\:{calculate}::\:\Theta:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{}\:=?? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 12/May/21
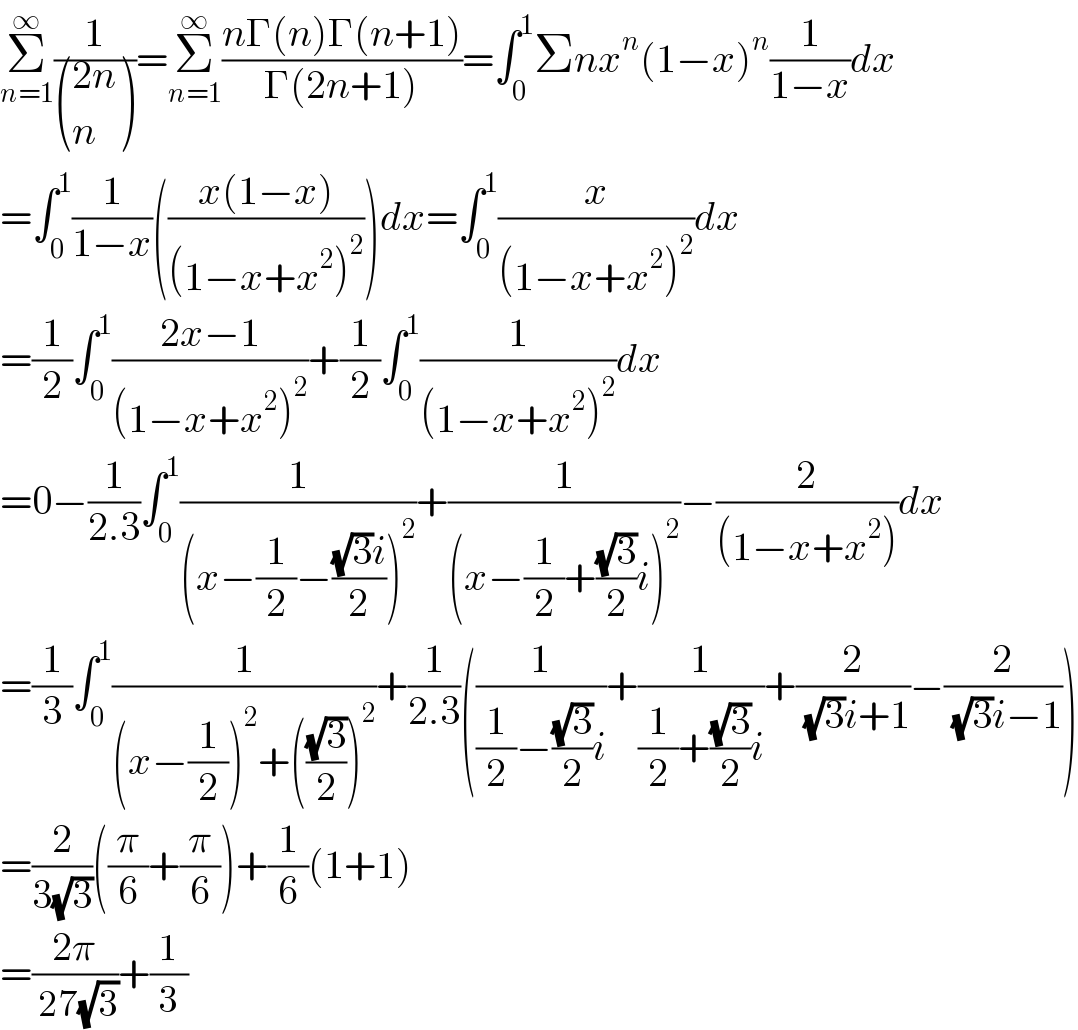
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}\Gamma\left({n}\right)\Gamma\left({n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \Sigma{nx}^{{n}} \left(\mathrm{1}−{x}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}}\left(\frac{{x}\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{0}−\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}}\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}}+\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}{i}+\mathrm{1}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}{i}−\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}\pi}{\:\mathrm{27}\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 12/May/21

$${thanks}\:{alot}... \\ $$
Answered by Ar Brandon last updated on 12/May/21
![S_n =Σ_(n=1) ^∞ (1/( ^(2n) C_n ))=Σ_(n=1) ^∞ ((n!×n!)/((2n)!))=Σ_(n=1) ^∞ ((Γ^2 (n+1))/(Γ(2n+1)))=Σ_(n=1) ^∞ nβ(n+1,n) =Σ_(n=1) ^∞ n∫_0 ^1 x^(n−1) (1−x)^n dx=∫_0 ^1 (1/x)Σ_(n=1) ^∞ n(x−x^2 )^n dx f(t)=Σ_(n=1) ^∞ t^n =(t/(1−t))⇒f ′(t)=Σ_(n=1) ^∞ nt^(n−1) =(1/((t−1)^2 )) S_n =∫_0 ^1 (1/x)∙((x−x^2 )/((x−x^2 −1)^2 ))dx=∫_0 ^1 ((1−x)/((x^2 −x+1)^2 ))dx Ostrogradsky gives S_n =(1/3)[((x+1)/(x^2 −x+1))+∫(dx/(x^2 −x+1))]_0 ^1 =[(1/3)∙((x+1)/(x^2 −x+1))+(2/( 3(√3)))arctan(((2x−1)/( (√3))))]_0 ^1 =(2/3)−(1/3)+(2/(3(√3)))((π/6)+(π/6))=(1/3)+((2π)/( 9(√3)))](Q140795.png)
$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\overset{\mathrm{2n}} {\:}\mathrm{C}_{\mathrm{n}} }=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}!×\mathrm{n}!}{\left(\mathrm{2n}\right)!}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\Gamma^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{2n}+\mathrm{1}\right)}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}\beta\left(\mathrm{n}+\mathrm{1},\mathrm{n}\right) \\ $$$$\:\:\:\:\:\:=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}} \mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}\left(\mathrm{x}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} \mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{t}^{\mathrm{n}} =\frac{\mathrm{t}}{\mathrm{1}−\mathrm{t}}\Rightarrow\mathrm{f}\:'\left(\mathrm{t}\right)=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{nt}^{\mathrm{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{S}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}}\centerdot\frac{\mathrm{x}−\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}−\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\: \\ $$$$\mathrm{Ostrogradsky}\:\mathrm{gives} \\ $$$$\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:=\left[\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\frac{\mathrm{2}}{\:\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{6}}\right)=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}\pi}{\:\mathrm{9}\sqrt{\mathrm{3}}} \\ $$
Commented by mnjuly1970 last updated on 12/May/21

$${grateful}... \\ $$
