
Question Number 126003 by mnjuly1970 last updated on 16/Dec/20

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{integral}... \\ $$$$\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\phi=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {tan}\left({x}\right){ln}\left({sin}\left({x}\right)\right){ln}\left({cos}\left({x}\right)\right){dx}=\frac{\zeta\left(\mathrm{3}\right.}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathscr{G}{ood}\:{luck} \\ $$
Answered by Olaf last updated on 16/Dec/20
![φ = ∫_0 ^(π/2) tanxln(cosx)ln(sinx)dx φ = −∫_0 ^(π/2) [−tanxln(cosx)]ln(sinx)dx φ = −[(1/2)ln^2 (cosx)ln(sinx)]_0 ^(π/2) +∫_0 ^(π/2) [(1/2)ln^2 (cosx)]cotxdx φ = (1/2)∫_0 ^(π/2) cotx.ln^2 (cosx)dx Let u = cosx du = −sinxdx = −(√(1−u^2 ))dx φ = (1/2)∫_1 ^0 (u/( (√(1−u^2 ))))ln^2 u(−(du/( (√(1−u^2 ))))) φ = (1/2)∫_0 ^1 (u/( 1−u^2 ))ln^2 udu φ = (1/2)∫_0 ^1 u.ln^2 uΣ_(n=0) ^∞ u^(2n) du φ = (1/2)Σ_(n=0) ^∞ ∫_0 ^1 u^(2n+1) ln^2 udu φ = (1/2)Σ_(n=0) ^∞ {[(u^(2n+2) /(2n+2))ln^2 u]_0 ^1 −∫_0 ^1 (u^(2n+2) /(2n+2))(2((lnu)/u))du} φ = (1/2)Σ_(n=0) ^∞ {−∫_0 ^1 (u^(2n+2) /(2n+2))(2((lnu)/u))du} φ = −Σ_(n=0) ^∞ ∫_0 ^1 (u^(2n+1) /(2n+2))lnudu φ = −Σ_(n=0) ^∞ {[(u^(2n+2) /((2n+2)^2 ))lnu]_0 ^1 −∫_0 ^1 (u^(2n+2) /((2n+2)^2 )).(du/u)} φ = Σ_(n=0) ^∞ ∫_0 ^1 (u^(2n+2) /((2n+2)^2 )).(du/u) φ = Σ_(n=0) ^∞ ∫_0 ^1 (u^(2n+1) /((2n+2)^2 )).du φ = Σ_(n=0) ^∞ [(u^(2n+2) /((2n+2)^3 ))]_0 ^1 φ = Σ_(n=0) ^∞ (1/((2n+2)^3 )) φ = (1/8)Σ_(n=0) ^∞ (1/((n+1)^3 )) φ = (1/8)Σ_(n=1) ^∞ (1/n^3 ) φ = ((ζ(3))/8)](Q126050.png)
$$\phi\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right)\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$$\phi\:=\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[−\mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right)\right]\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$$\phi\:=\:−\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{cos}{x}\right)\mathrm{ln}\left(\mathrm{sin}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{cos}{x}\right)\right]\mathrm{cot}{xdx} \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cot}{x}.\mathrm{ln}^{\mathrm{2}} \left(\mathrm{cos}{x}\right){dx} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{cos}{x} \\ $$$${du}\:=\:−\mathrm{sin}{xdx}\:=\:−\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }{dx} \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{0}} \frac{{u}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\mathrm{ln}^{\mathrm{2}} {u}\left(−\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\right) \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}}{\:\mathrm{1}−{u}^{\mathrm{2}} }\mathrm{ln}^{\mathrm{2}} {udu} \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}.\mathrm{ln}^{\mathrm{2}} {u}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{u}^{\mathrm{2}{n}} {du} \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{2}{n}+\mathrm{1}} \mathrm{ln}^{\mathrm{2}} {udu} \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\left[\frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}+\mathrm{2}}\mathrm{ln}^{\mathrm{2}} {u}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}+\mathrm{2}}\left(\mathrm{2}\frac{\mathrm{ln}{u}}{{u}}\right){du}\right\} \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}+\mathrm{2}}\left(\mathrm{2}\frac{\mathrm{ln}{u}}{{u}}\right){du}\right\} \\ $$$$\phi\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{2}}\mathrm{ln}{udu} \\ $$$$\phi\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\left[\frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{2}} }\mathrm{ln}{u}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{2}} }.\frac{{du}}{{u}}\right\} \\ $$$$\phi\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{2}} }.\frac{{du}}{{u}} \\ $$$$\phi\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{2}} }.{du} \\ $$$$\phi\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\phi\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{3}} } \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\phi\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$\phi\:=\:\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$
Commented by mnjuly1970 last updated on 16/Dec/20
$${thanks}\:{alot}\:{sir}\:{olaf}... \\ $$
Answered by Lordose last updated on 16/Dec/20
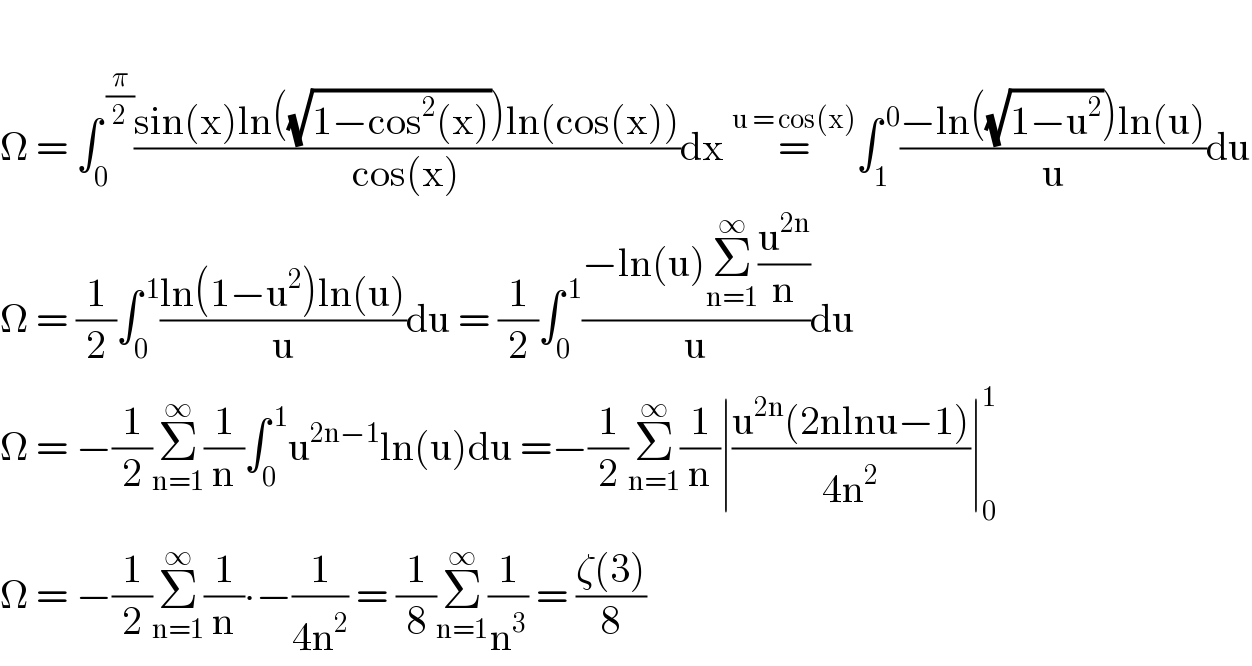
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\left(\mathrm{x}\right)\mathrm{ln}\left(\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)}\right)\mathrm{ln}\left(\mathrm{cos}\left(\mathrm{x}\right)\right)}{\mathrm{cos}\left(\mathrm{x}\right)}\mathrm{dx}\:\overset{\mathrm{u}\:=\:\mathrm{cos}\left(\mathrm{x}\right)} {=}\int_{\mathrm{1}} ^{\:\mathrm{0}} \frac{−\mathrm{ln}\left(\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\right)\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{u}}\mathrm{du} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{u}}\mathrm{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{−\mathrm{ln}\left(\mathrm{u}\right)\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{u}^{\mathrm{2n}} }{\mathrm{n}}}{\mathrm{u}}\mathrm{du} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{2n}−\mathrm{1}} \mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}\:=−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\mid\frac{\mathrm{u}^{\mathrm{2n}} \left(\mathrm{2nlnu}−\mathrm{1}\right)}{\mathrm{4n}^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\centerdot−\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:=\:\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$
Commented by mnjuly1970 last updated on 16/Dec/20
$${excellent}\:{sir}\:{lordose}... \\ $$
