
Question Number 143454 by mnjuly1970 last updated on 14/Jun/21

$$ \\ $$$$\:\:\:........{nice}\:.......{integral}....... \\ $$$$\:\:\mathscr{T}\:\::=\int_{\mathrm{0}} ^{\:\infty} \frac{{arctan}\left({x}\right)}{{x}^{\:{ln}\left({x}\right)\:+\mathrm{1}} }{dx}\overset{?} {=}\frac{\pi\sqrt{\pi}}{\mathrm{4}} \\ $$$$ \\ $$
Answered by mindispower last updated on 14/Jun/21
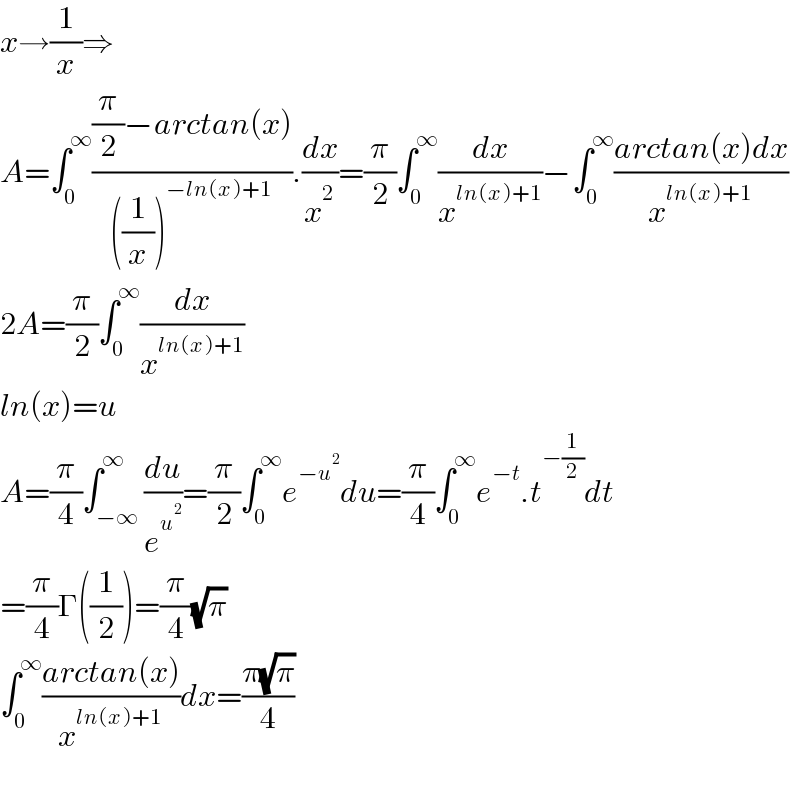
$${x}\rightarrow\frac{\mathrm{1}}{{x}}\Rightarrow \\ $$$${A}=\int_{\mathrm{0}} ^{\infty} \frac{\frac{\pi}{\mathrm{2}}−{arctan}\left({x}\right)}{\left(\frac{\mathrm{1}}{{x}}\right)^{−{ln}\left({x}\right)+\mathrm{1}} }.\frac{{dx}}{{x}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{{ln}\left({x}\right)+\mathrm{1}} }−\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left({x}\right){dx}}{{x}^{{ln}\left({x}\right)+\mathrm{1}} } \\ $$$$\mathrm{2}{A}=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{{ln}\left({x}\right)+\mathrm{1}} } \\ $$$${ln}\left({x}\right)={u} \\ $$$${A}=\frac{\pi}{\mathrm{4}}\int_{−\infty} ^{\infty} \frac{{du}}{{e}^{{u}^{\mathrm{2}} } }=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}^{\mathrm{2}} } {du}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} .{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\frac{\pi}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}}\sqrt{\pi} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left({x}\right)}{{x}^{{ln}\left({x}\right)+\mathrm{1}} }{dx}=\frac{\pi\sqrt{\pi}}{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 14/Jun/21

$${thankd}\:{alot}.. \\ $$
Commented by mindispower last updated on 14/Jun/21

$${pleasur} \\ $$
