
Question Number 126109 by mnjuly1970 last updated on 17/Dec/20
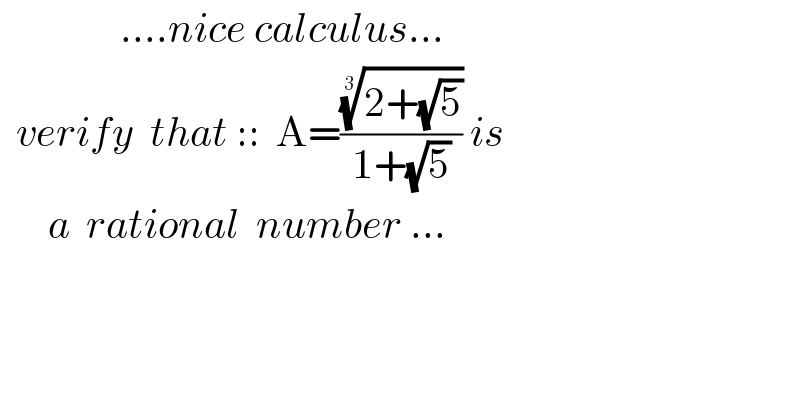
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....{nice}\:{calculus}... \\ $$$$\:\:{verify}\:\:{that}\:::\:\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}}{\mathrm{1}+\sqrt{\mathrm{5}}}\:{is} \\ $$$$\:\:\:\:\:\:{a}\:\:{rational}\:\:{number}\:... \\ $$
Answered by som(math1967) last updated on 17/Dec/20
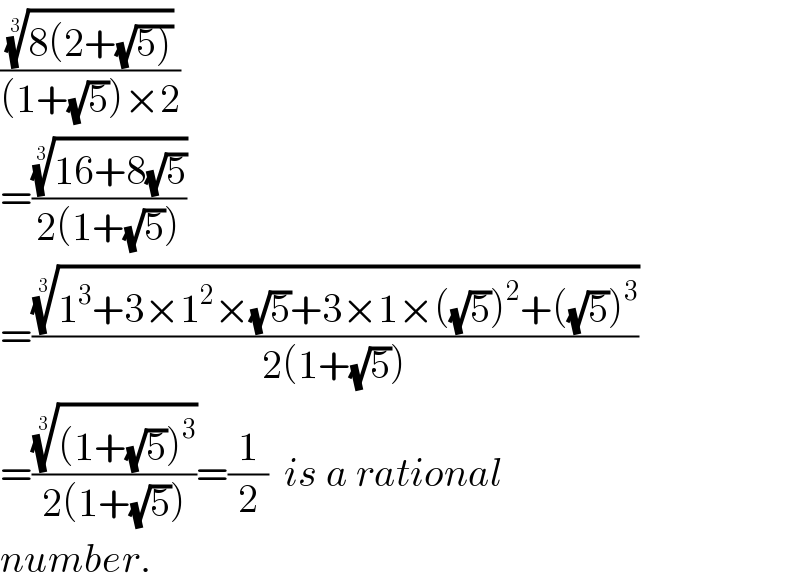
$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{8}\left(\mathrm{2}+\sqrt{\left.\mathrm{5}\right)}\right.}}{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)×\mathrm{2}} \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{\mathrm{16}+\mathrm{8}\sqrt{\mathrm{5}}}}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}^{\mathrm{3}} +\mathrm{3}×\mathrm{1}^{\mathrm{2}} ×\sqrt{\mathrm{5}}+\mathrm{3}×\mathrm{1}×\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{5}}\right)^{\mathrm{3}} }}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{3}} }}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\:\:{is}\:{a}\:{rational} \\ $$$${number}. \\ $$
Commented by mnjuly1970 last updated on 17/Dec/20

$${thanks}\:{alot} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Dec/20
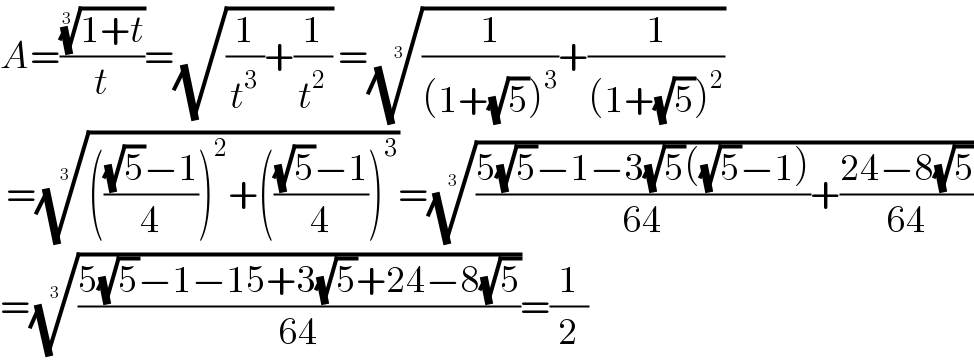
$${A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+{t}}}{{t}}=\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\:=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }} \\ $$$$\:=\sqrt[{\mathrm{3}}]{\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} }=\sqrt[{\mathrm{3}}]{\frac{\mathrm{5}\sqrt{\mathrm{5}}−\mathrm{1}−\mathrm{3}\sqrt{\mathrm{5}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}{\mathrm{64}}+\frac{\mathrm{24}−\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{64}}} \\ $$$$=\sqrt[{\mathrm{3}}]{\frac{\mathrm{5}\sqrt{\mathrm{5}}−\mathrm{1}−\mathrm{15}+\mathrm{3}\sqrt{\mathrm{5}}+\mathrm{24}−\mathrm{8}\sqrt{\mathrm{5}}}{\mathrm{64}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 17/Dec/20

$${grateful}\:... \\ $$
