
Question Number 136626 by mnjuly1970 last updated on 24/Mar/21
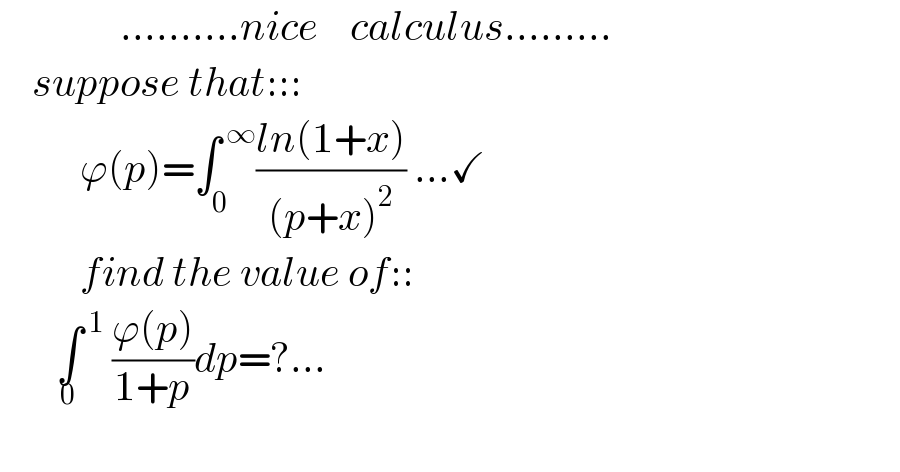
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..........{nice}\:\:\:\:{calculus}......... \\ $$$$\:\:\:\:{suppose}\:{that}::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\varphi\left({p}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\left({p}+{x}\right)^{\mathrm{2}} }\:...\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:{find}\:{the}\:{value}\:{of}:: \\ $$$$\:\:\:\:\:\:\:\underset{\mathrm{0}} {\int}^{\:\mathrm{1}} \:\frac{\varphi\left({p}\right)}{\mathrm{1}+{p}}{dp}=?... \\ $$$$\:\:\:\:\:\: \\ $$
Answered by mindispower last updated on 24/Mar/21
![ϕ(p)=∫_0 ^∞ (dx/((p+x)(1+x))) =(1/(p−1))[ln(((1+x)/(p+x)))]_0 ^∞ =((ln(p))/(p−1)) ∫_0 ^1 ((−ln(p))/((1−p^2 )))dp=−∫_0 ^1 Σ_(n≥0) p^(2n) ln(p)dp =Σ(1/((2n+1)^2 ))=(3/4)𝛇(2)=(π^2 /8)](Q136630.png)
$$\varphi\left({p}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({p}+{x}\right)\left(\mathrm{1}+{x}\right)}\:=\frac{\mathrm{1}}{{p}−\mathrm{1}}\left[{ln}\left(\frac{\mathrm{1}+{x}}{{p}+{x}}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{{ln}\left({p}\right)}{{p}−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{ln}\left({p}\right)}{\left(\mathrm{1}−{p}^{\mathrm{2}} \right)}{dp}=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{0}} {\sum}{p}^{\mathrm{2}{n}} {ln}\left({p}\right){dp} \\ $$$$=\Sigma\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}}\boldsymbol{\zeta}\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 24/Mar/21
$$\:\:{tashakor}\:.{grateful}..{sir}\:{power}.. \\ $$
