
Question Number 124831 by mnjuly1970 last updated on 06/Dec/20
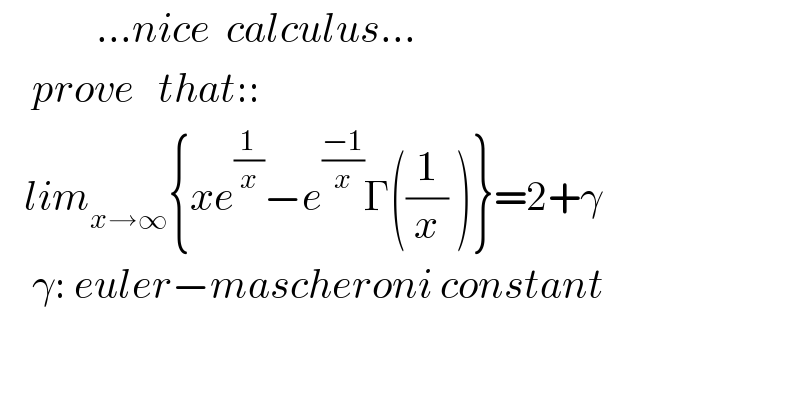
$$\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:\:{prove}\:\:\:{that}:: \\ $$$$\:\:\:{lim}_{{x}\rightarrow\infty} \left\{{xe}^{\frac{\mathrm{1}}{{x}}} −{e}^{\frac{−\mathrm{1}}{{x}}} \Gamma\left(\frac{\mathrm{1}}{{x}}\:\right)\right\}=\mathrm{2}+\gamma \\ $$$$\:\:\:\:\gamma:\:{euler}−{mascheroni}\:{constant} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 06/Dec/20
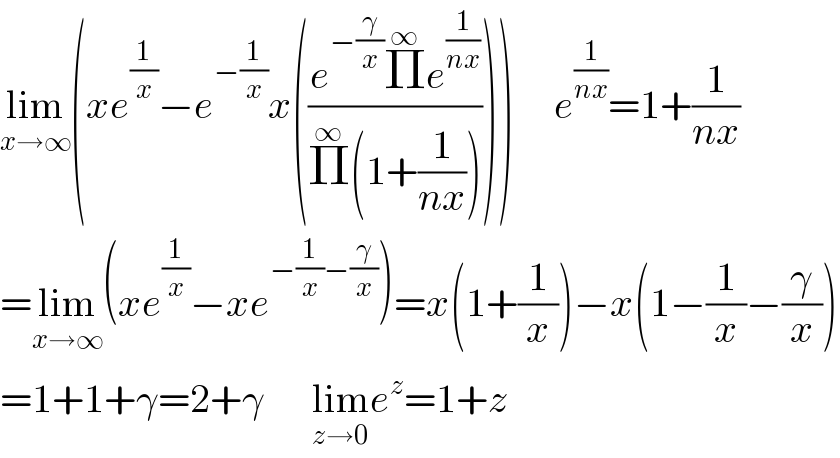
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({xe}^{\frac{\mathrm{1}}{{x}}} −{e}^{−\frac{\mathrm{1}}{{x}}} {x}\left(\frac{{e}^{−\frac{\gamma}{{x}}} \overset{\infty} {\prod}{e}^{\frac{\mathrm{1}}{{nx}}} }{\overset{\infty} {\prod}\left(\mathrm{1}+\frac{\mathrm{1}}{{nx}}\right)}\right)\right)\:\:\:\:\:{e}^{\frac{\mathrm{1}}{{nx}}} =\mathrm{1}+\frac{\mathrm{1}}{{nx}} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({xe}^{\frac{\mathrm{1}}{{x}}} −{xe}^{−\frac{\mathrm{1}}{{x}}−\frac{\gamma}{{x}}} \right)={x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)−{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}−\frac{\gamma}{{x}}\right) \\ $$$$=\mathrm{1}+\mathrm{1}+\gamma=\mathrm{2}+\gamma\:\:\:\:\:\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{{z}} =\mathrm{1}+{z} \\ $$
Commented by mnjuly1970 last updated on 06/Dec/20

$${thank}\:{you} \\ $$$${excellent}.... \\ $$
Commented by Dwaipayan Shikari last updated on 06/Dec/20

$$\left.{Great}\:{sir}!\:\::\right) \\ $$
Answered by mindispower last updated on 06/Dec/20
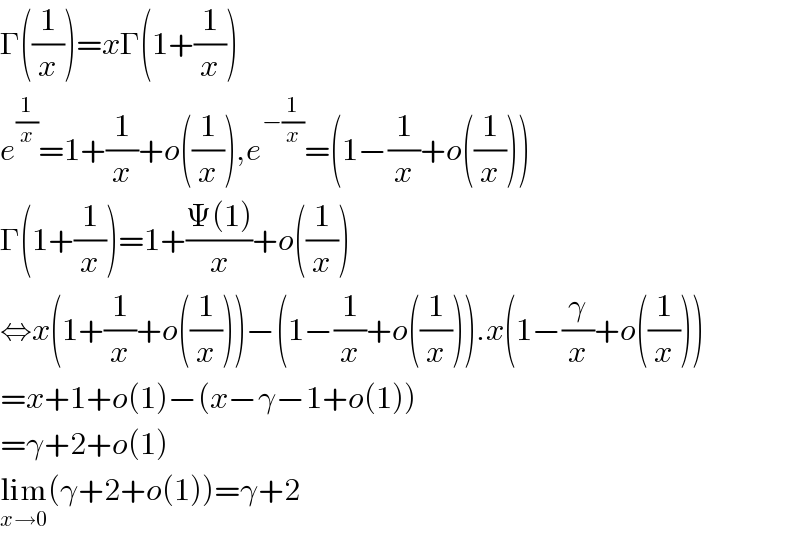
$$\Gamma\left(\frac{\mathrm{1}}{{x}}\right)={x}\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${e}^{\frac{\mathrm{1}}{{x}}} =\mathrm{1}+\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right),{e}^{−\frac{\mathrm{1}}{{x}}} =\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right) \\ $$$$\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{1}+\frac{\Psi\left(\mathrm{1}\right)}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Leftrightarrow{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right).{x}\left(\mathrm{1}−\frac{\gamma}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\right)\: \\ $$$$={x}+\mathrm{1}+{o}\left(\mathrm{1}\right)−\left({x}−\gamma−\mathrm{1}+{o}\left(\mathrm{1}\right)\right) \\ $$$$=\gamma+\mathrm{2}+{o}\left(\mathrm{1}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\gamma+\mathrm{2}+{o}\left(\mathrm{1}\right)\right)=\gamma+\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 06/Dec/20
$${thanks}\:{alot}\:{sir}\:{Powr}.. \\ $$
Answered by mnjuly1970 last updated on 06/Dec/20
![(1/x)=_(t→0) ^(x→∞) t lim_(t→0) [(1/t)e^t −e^(−t) Γ(t)] =lim_(t→0) (((e^t −e^(−t) Γ(t+1))/t)) =_(rule) ^(hopital) lim_(t→0) (((e^t +e^(−t) Γ(t+1)−Γ′(t+1)e^(−t) )/1)) =1+1−ψ(1)=2−(−γ)=2+γ ✓](Q124871.png)
$$\frac{\mathrm{1}}{{x}}\underset{{t}\rightarrow\mathrm{0}} {\overset{{x}\rightarrow\infty} {=}}{t} \\ $$$$\:\:{lim}_{{t}\rightarrow\mathrm{0}} \left[\frac{\mathrm{1}}{{t}}{e}^{{t}} −{e}^{−{t}} \Gamma\left({t}\right)\right] \\ $$$$\:\:={lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{e}^{{t}} −{e}^{−{t}} \Gamma\left({t}+\mathrm{1}\right)}{{t}}\right) \\ $$$$\:\underset{{rule}} {\overset{{hopital}} {=}}{lim}_{{t}\rightarrow\mathrm{0}} \left(\frac{{e}^{{t}} +{e}^{−{t}} \Gamma\left({t}+\mathrm{1}\right)−\Gamma'\left({t}+\mathrm{1}\right){e}^{−{t}} }{\mathrm{1}}\right) \\ $$$$=\mathrm{1}+\mathrm{1}−\psi\left(\mathrm{1}\right)=\mathrm{2}−\left(−\gamma\right)=\mathrm{2}+\gamma\:\checkmark \\ $$
