Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 134272 by mnjuly1970 last updated on 01/Mar/21

nice calculus prove that: : i :: =∫_0 ^( ∞) ((cos(πx))/(e^(2π(√x) ) −1)) dx=((2−(√2) )/8) ii:: compute: Σ_(n=−∞) ^∞ (1/(n^4 +9n^2 +10)) =? ...m.n...

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{nice}\:\:\:\mathrm{calculus} \\ $$$$\:\:\:\:\mathrm{prove}\:\mathrm{that}:\::\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{i}\:::\:\: =\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left(\pi{x}\right)}{{e}^{\mathrm{2}\pi\sqrt{{x}}\:} −\mathrm{1}}\:{dx}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}\:}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ii}::\:{compute}:\:\:\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} +\mathrm{9}{n}^{\mathrm{2}} +\mathrm{10}}\:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}... \\ $$

Answered by Dwaipayan Shikari last updated on 01/Mar/21

Commented by Dwaipayan Shikari last updated on 01/Mar/21

Ramanujan′s letter

$${Ramanujan}'{s}\:{letter}\: \\ $$

Commented by mnjuly1970 last updated on 02/Mar/21

thank you..

$$\:\:{thank}\:{you}.. \\ $$

Answered by Dwaipayan Shikari last updated on 01/Mar/21

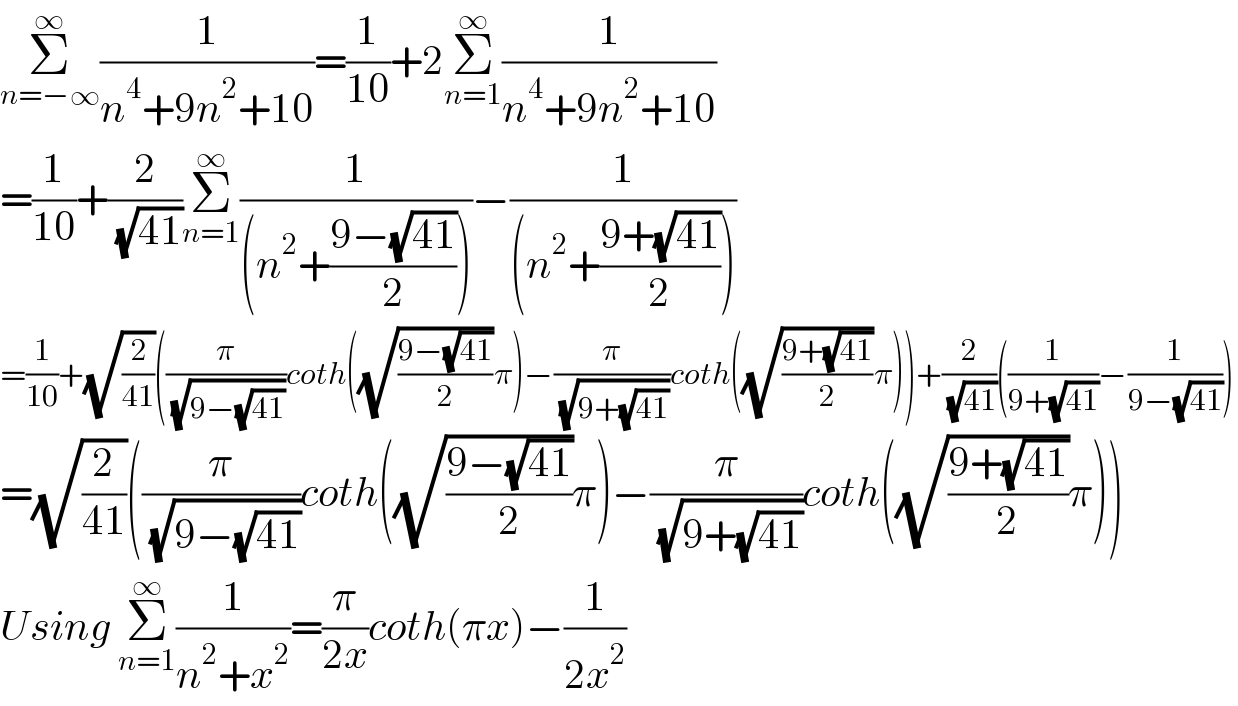
Σ_(n=−∞) ^∞ (1/(n^4 +9n^2 +10))=(1/(10))+2Σ_(n=1) ^∞ (1/(n^4 +9n^2 +10)) =(1/(10))+(2/( (√(41))))Σ_(n=1) ^∞ (1/((n^2 +((9−(√(41)))/2))))−(1/((n^2 +((9+(√(41)))/2)))) =(1/(10))+(√(2/(41)))((π/( (√(9−(√(41))))))coth((√((9−(√(41)))/2))π)−(π/( (√(9+(√(41))))))coth((√((9+(√(41)))/2))π))+(2/( (√(41))))((1/(9+(√(41))))−(1/(9−(√(41))))) =(√(2/(41)))((π/( (√(9−(√(41))))))coth((√((9−(√(41)))/2))π)−(π/( (√(9+(√(41))))))coth((√((9+(√(41)))/2))π)) Using Σ_(n=1) ^∞ (1/(n^2 +x^2 ))=(π/(2x))coth(πx)−(1/(2x^2 ))

$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} +\mathrm{9}{n}^{\mathrm{2}} +\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{10}}+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} +\mathrm{9}{n}^{\mathrm{2}} +\mathrm{10}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{41}}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +\frac{\mathrm{9}−\sqrt{\mathrm{41}}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +\frac{\mathrm{9}+\sqrt{\mathrm{41}}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}+\sqrt{\frac{\mathrm{2}}{\mathrm{41}}}\left(\frac{\pi}{\:\sqrt{\mathrm{9}−\sqrt{\mathrm{41}}}}{coth}\left(\sqrt{\frac{\mathrm{9}−\sqrt{\mathrm{41}}}{\mathrm{2}}}\pi\right)−\frac{\pi}{\:\sqrt{\mathrm{9}+\sqrt{\mathrm{41}}}}{coth}\left(\sqrt{\frac{\mathrm{9}+\sqrt{\mathrm{41}}}{\mathrm{2}}}\pi\right)\right)+\frac{\mathrm{2}}{\:\sqrt{\mathrm{41}}}\left(\frac{\mathrm{1}}{\mathrm{9}+\sqrt{\mathrm{41}}}−\frac{\mathrm{1}}{\mathrm{9}−\sqrt{\mathrm{41}}}\right) \\ $$$$=\sqrt{\frac{\mathrm{2}}{\mathrm{41}}}\left(\frac{\pi}{\:\sqrt{\mathrm{9}−\sqrt{\mathrm{41}}}}{coth}\left(\sqrt{\frac{\mathrm{9}−\sqrt{\mathrm{41}}}{\mathrm{2}}}\pi\right)−\frac{\pi}{\:\sqrt{\mathrm{9}+\sqrt{\mathrm{41}}}}{coth}\left(\sqrt{\frac{\mathrm{9}+\sqrt{\mathrm{41}}}{\mathrm{2}}}\pi\right)\right) \\ $$$${Using}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{x}}{coth}\left(\pi{x}\right)−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com