
Question Number 126986 by mnjuly1970 last updated on 25/Dec/20
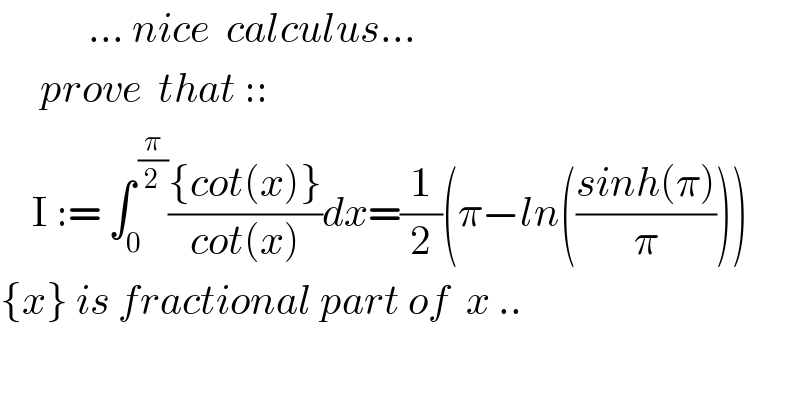
$$\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:{calculus}... \\ $$$$\:\:\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\left\{{cot}\left({x}\right)\right\}}{{cot}\left({x}\right)}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\left(\pi−{ln}\left(\frac{{sinh}\left(\pi\right)}{\pi}\right)\right) \\ $$$$\left\{{x}\right\}\:{is}\:{fractional}\:{part}\:{of}\:\:{x}\:.. \\ $$
Answered by Olaf last updated on 26/Dec/20
![I = ∫_0 ^(π/2) (({cotx})/(cotx))dx Let u = cotx I = ∫_∞ ^0 (({u})/u).(du/((−1−u^2 ))) I = ∫_0 ^∞ (({u})/(u(1+u^2 )))du I = Σ_(n=0) ^∞ ∫_n ^(n+1) (({u})/(u(1+u^2 )))du I = Σ_(n=0) ^∞ ∫_n ^(n+1) ((u−n)/(u(1+u^2 )))du I = Σ_(n=0) ^∞ ∫_n ^(n+1) [((nu+1)/(u^2 +1))−(n/u)]du I = Σ_(n=0) ^∞ [(n/2)ln(1+u^2 )−arctanu−nlnu]_n ^(n+1) ...to be continued...](Q127055.png)
$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left\{\mathrm{cot}{x}\right\}}{\mathrm{cot}{x}}{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{cot}{x} \\ $$$$\mathrm{I}\:=\:\int_{\infty} ^{\mathrm{0}} \frac{\left\{{u}\right\}}{{u}}.\frac{{du}}{\left(−\mathrm{1}−{u}^{\mathrm{2}} \right)} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\left\{{u}\right\}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \frac{\left\{{u}\right\}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \frac{{u}−{n}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \left[\frac{{nu}+\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}−\frac{{n}}{{u}}\right]{du} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{n}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)−\mathrm{arctan}{u}−{n}\mathrm{ln}{u}\right]_{{n}} ^{{n}+\mathrm{1}} \\ $$$$...{to}\:{be}\:{continued}... \\ $$
