
Question Number 116744 by mnjuly1970 last updated on 06/Oct/20
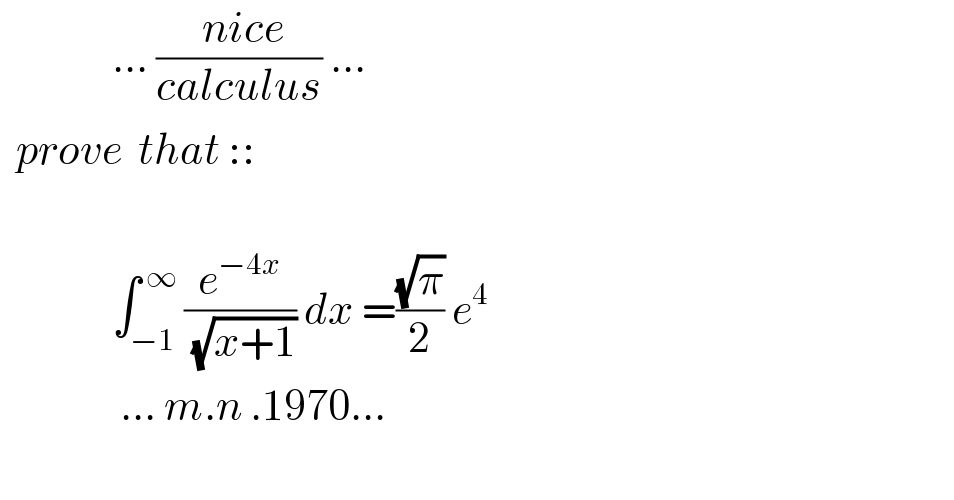
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:\frac{\:{nice}}{{calculus}}\:... \\ $$$$\:\:{prove}\:\:{that}\::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{−\mathrm{1}} ^{\:\infty} \frac{{e}^{−\mathrm{4}{x}} }{\:\sqrt{{x}+\mathrm{1}}}\:{dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{m}.{n}\:.\mathrm{1970}... \\ $$$$ \\ $$
Answered by mindispower last updated on 06/Oct/20
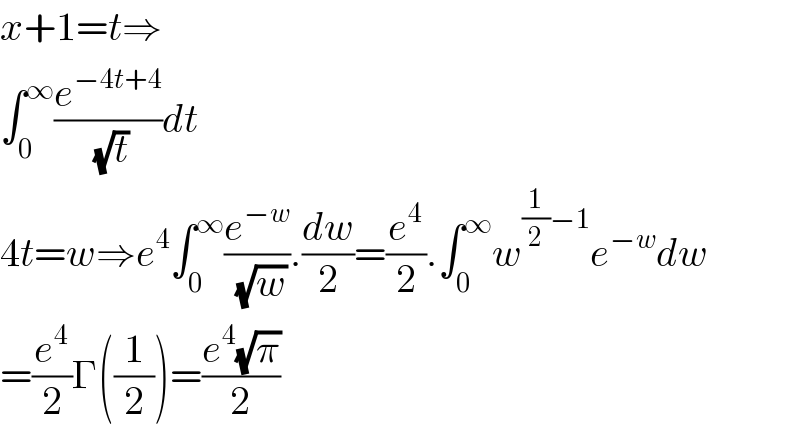
$${x}+\mathrm{1}={t}\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{4}{t}+\mathrm{4}} }{\:\sqrt{{t}}}{dt} \\ $$$$\mathrm{4}{t}={w}\Rightarrow{e}^{\mathrm{4}} \int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{w}} }{\:\sqrt{{w}}}.\frac{{dw}}{\mathrm{2}}=\frac{{e}^{\mathrm{4}} }{\mathrm{2}}.\int_{\mathrm{0}} ^{\infty} {w}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {e}^{−{w}} {dw} \\ $$$$=\frac{{e}^{\mathrm{4}} }{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{{e}^{\mathrm{4}} \sqrt{\pi}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 06/Oct/20
$${thank}\:{you}\:{so}\:{much}\:... \\ $$
Answered by Dwaipayan Shikari last updated on 06/Oct/20
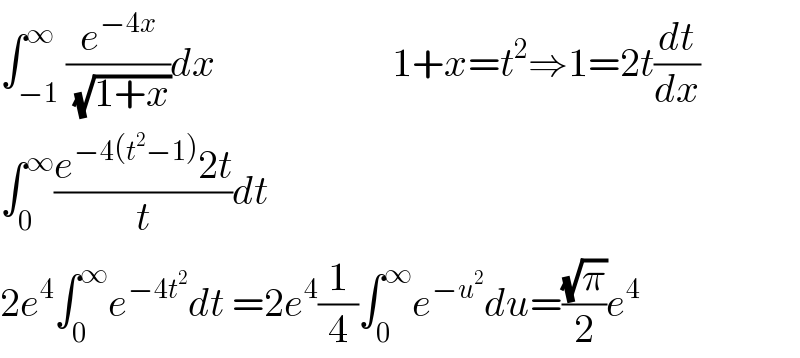
$$\int_{−\mathrm{1}} ^{\infty} \frac{{e}^{−\mathrm{4}{x}} }{\:\sqrt{\mathrm{1}+{x}}}{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}+{x}={t}^{\mathrm{2}} \Rightarrow\mathrm{1}=\mathrm{2}{t}\frac{{dt}}{{dx}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{1}\right)} \mathrm{2}{t}}{{t}}{dt} \\ $$$$\mathrm{2}{e}^{\mathrm{4}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{4}{t}^{\mathrm{2}} } {dt}\:=\mathrm{2}{e}^{\mathrm{4}} \frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}^{\mathrm{2}} } {du}=\frac{\sqrt{\pi}}{\mathrm{2}}{e}^{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 06/Oct/20

$${grateful}.. \\ $$
Answered by 1549442205PVT last updated on 06/Oct/20
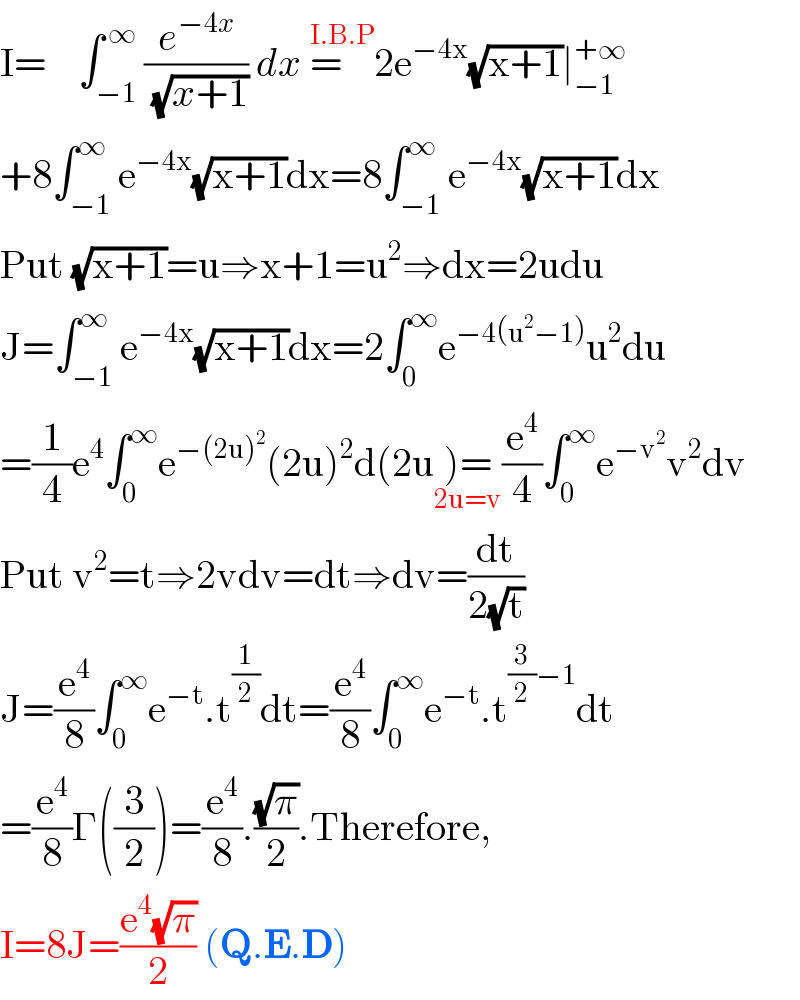
$$\mathrm{I}=\:\:\:\:\int_{−\mathrm{1}} ^{\:\infty} \frac{{e}^{−\mathrm{4}{x}} }{\:\sqrt{{x}+\mathrm{1}}}\:{dx}\:\overset{\mathrm{I}.\mathrm{B}.\mathrm{P}} {=\:\:\:\:}\mathrm{2e}^{−\mathrm{4x}} \sqrt{\mathrm{x}+\mathrm{1}}\mid_{−\mathrm{1}} ^{+\infty} \\ $$$$+\mathrm{8}\int_{−\mathrm{1}} ^{\infty} \mathrm{e}^{−\mathrm{4x}} \sqrt{\mathrm{x}+\mathrm{1}}\mathrm{dx}=\mathrm{8}\int_{−\mathrm{1}} ^{\infty} \mathrm{e}^{−\mathrm{4x}} \sqrt{\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{Put}\:\sqrt{\mathrm{x}+\mathrm{1}}=\mathrm{u}\Rightarrow\mathrm{x}+\mathrm{1}=\mathrm{u}^{\mathrm{2}} \Rightarrow\mathrm{dx}=\mathrm{2udu} \\ $$$$\mathrm{J}=\int_{−\mathrm{1}} ^{\infty} \mathrm{e}^{−\mathrm{4x}} \sqrt{\mathrm{x}+\mathrm{1}}\mathrm{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{4}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)} \mathrm{u}^{\mathrm{2}} \mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{4}} \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{2u}\right)^{\mathrm{2}} } \left(\mathrm{2u}\right)^{\mathrm{2}} \mathrm{d}\left(\mathrm{2u}\underset{\mathrm{2u}=\mathrm{v}} {\right)=}\frac{\mathrm{e}^{\mathrm{4}} }{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{v}^{\mathrm{2}} } \mathrm{v}^{\mathrm{2}} \mathrm{dv} \\ $$$$\mathrm{Put}\:\mathrm{v}^{\mathrm{2}} =\mathrm{t}\Rightarrow\mathrm{2vdv}=\mathrm{dt}\Rightarrow\mathrm{dv}=\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}} \\ $$$$\mathrm{J}=\frac{\mathrm{e}^{\mathrm{4}} }{\mathrm{8}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} .\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dt}=\frac{\mathrm{e}^{\mathrm{4}} }{\mathrm{8}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} .\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \mathrm{dt} \\ $$$$=\frac{\mathrm{e}^{\mathrm{4}} }{\mathrm{8}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{e}^{\mathrm{4}} }{\mathrm{8}}.\frac{\sqrt{\pi}}{\mathrm{2}}.\mathrm{Therefore}, \\ $$$$\mathrm{I}=\mathrm{8J}=\frac{\mathrm{e}^{\mathrm{4}} \sqrt{\pi}}{\mathrm{2}}\:\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$
Commented by mnjuly1970 last updated on 06/Oct/20

$${thank}\:{you}... \\ $$
Commented by 1549442205PVT last updated on 07/Oct/20

$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mathmax by abdo last updated on 06/Oct/20
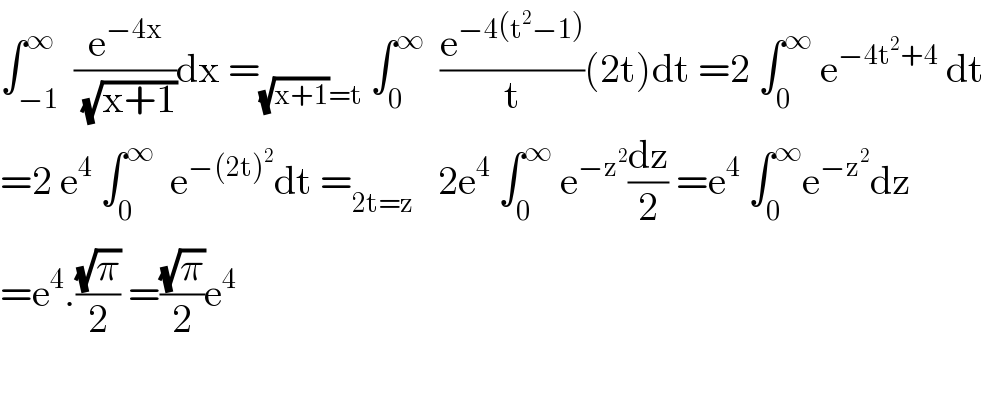
$$\int_{−\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{4x}} }{\sqrt{\mathrm{x}+\mathrm{1}}}\mathrm{dx}\:=_{\sqrt{\mathrm{x}+\mathrm{1}}=\mathrm{t}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{4}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)} }{\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4t}^{\mathrm{2}} +\mathrm{4}} \:\mathrm{dt} \\ $$$$=\mathrm{2}\:\mathrm{e}^{\mathrm{4}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\left(\mathrm{2t}\right)^{\mathrm{2}} } \mathrm{dt}\:=_{\mathrm{2t}=\mathrm{z}} \:\:\:\mathrm{2e}^{\mathrm{4}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\mathrm{2}}\:=\mathrm{e}^{\mathrm{4}} \:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz} \\ $$$$=\mathrm{e}^{\mathrm{4}} .\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{e}^{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 06/Oct/20
$${grateful}\:\:{sir}\:.. \\ $$$$\:{very}\:\:{nice}\:\:{as}\:\:{always}.. \\ $$
Commented by Bird last updated on 07/Oct/20
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
