
Question Number 131401 by mnjuly1970 last updated on 04/Feb/21
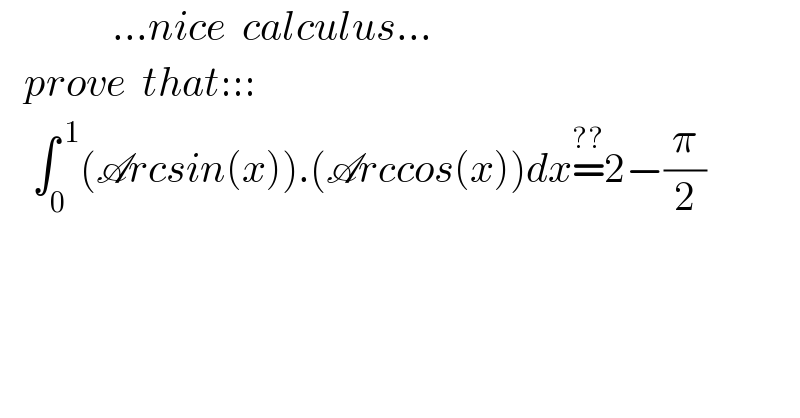
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:{prove}\:\:{that}::: \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathscr{A}{rcsin}\left({x}\right)\right).\left(\mathscr{A}{rccos}\left({x}\right)\right){dx}\overset{??} {=}\mathrm{2}−\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 04/Feb/21
![Φ=∫_0 ^1 (arcsinx)(arcosx)dx ⇒Φ =∫_0 ^(1 ) arcsinx((π/2)−arcsinx)dx =(π/2)∫_0 ^1 arcsinx dx −∫_0 ^1 arcsin^2 x dx ∫_0 ^1 arcsinx dx =_(arcsinx=t) ∫_0 ^(π/2) t.cost dt =_(byparts) [tsint]_0 ^(π/2) −∫_0 ^(π/2) sint dt =(π/2) +[cost]_0 ^(π/2) =(π/2)−1 ∫_0 ^1 (arcsinx)^2 dx =_(arcsinx=t) ∫_0 ^(π/2) t^2 cost dt =[t^2 sint]_0 ^(π/2) −2∫_0 ^(π/2) t sint dt =(π^2 /4)−2{ [−tcost]_0 ^(π/2) +∫_0 ^(π/2) cost dt} =(π^2 /4)−2[sint]_0 ^(π/2) =(π^2 /4)−2 ⇒Φ=(π/2)((π/2)−1)−(π^2 /4)+2 ⇒ Φ=2−(π/2)](Q131416.png)
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{arcsinx}\right)\left(\mathrm{arcosx}\right)\mathrm{dx}\:\Rightarrow\Phi\:=\int_{\mathrm{0}} ^{\mathrm{1}\:} \mathrm{arcsinx}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arcsinx}\right)\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{arcsinx}\:\mathrm{dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{arcsin}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{arcsinx}\:\mathrm{dx}\:=_{\mathrm{arcsinx}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{t}.\mathrm{cost}\:\mathrm{dt}\:=_{\mathrm{byparts}} \:\:\left[\mathrm{tsint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sint}\:\mathrm{dt} \\ $$$$=\frac{\pi}{\mathrm{2}}\:+\left[\mathrm{cost}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{arcsinx}\right)^{\mathrm{2}} \mathrm{dx}\:=_{\mathrm{arcsinx}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{t}^{\mathrm{2}} \mathrm{cost}\:\mathrm{dt} \\ $$$$=\left[\mathrm{t}^{\mathrm{2}} \mathrm{sint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{t}\:\mathrm{sint}\:\mathrm{dt}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{2}\left\{\:\left[−\mathrm{tcost}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cost}\:\mathrm{dt}\right\} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{2}\left[\mathrm{sint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{2}\:\Rightarrow\Phi=\frac{\pi}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{1}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}+\mathrm{2}\:\Rightarrow \\ $$$$\Phi=\mathrm{2}−\frac{\pi}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 04/Feb/21
$${thank}\:{you}\:{so}\:{much} \\ $$$${sir}\:{max}... \\ $$
Commented by mathmax by abdo last updated on 04/Feb/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
