
Question Number 129806 by mnjuly1970 last updated on 19/Jan/21
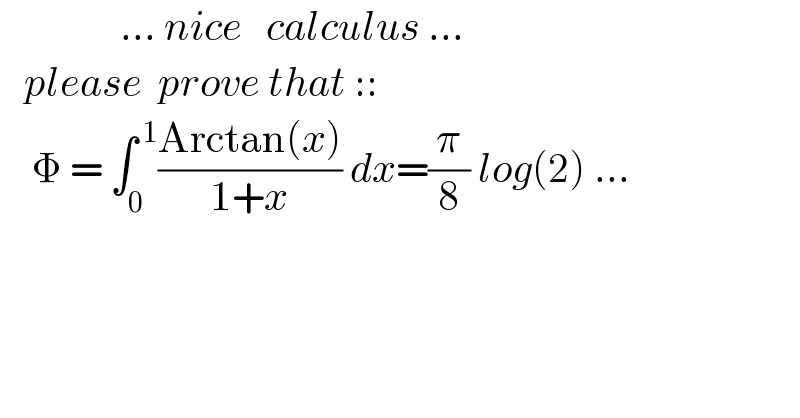
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:\:{calculus}\:... \\ $$$$\:\:\:{please}\:\:{prove}\:{that}\::: \\ $$$$\:\:\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{Arctan}\left({x}\right)}{\mathrm{1}+{x}}\:{dx}=\frac{\pi}{\mathrm{8}}\:{log}\left(\mathrm{2}\right)\:... \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 19/Jan/21
![[tan^(−1) (x)log(x+1)]_0 ^1 −∫_0 ^1 ((log(x+1))/(x^2 +1))dx =(π/4)log(2)−∫_0 ^(π/4) log(1+tanθ)dθ =(π/4)log(2)−(π/8)log(2) =(π/8)log(2)](Q129812.png)
$$\left[{tan}^{−\mathrm{1}} \left({x}\right){log}\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}{log}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{log}\left(\mathrm{1}+{tan}\theta\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{4}}{log}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right) \\ $$$$=\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right) \\ $$
Commented by mnjuly1970 last updated on 19/Jan/21

$${nice}\:{very}\:{nice}.. \\ $$
Answered by mnjuly1970 last updated on 19/Jan/21

Answered by mathmax by abdo last updated on 19/Jan/21
![Φ=∫_0 ^1 ((arctanx)/(1+x))dx by parts Φ=[ln(1+x)arctanx]_0 ^1 −∫_0 ^1 ln(1+x)×(dx/(1+x^2 )) =(π/4)ln(2)−∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx we hsve ∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx =_(x=tanθ) ∫_0 ^(π/4) ((ln(1+tanθ))/(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^(π/4) ln(1+tanθ)dθ =_(θ=(π/4)−u) ∫_0 ^(π/4) ln(1+((1−tanu)/(1+tanu)))du =∫_0 ^(π/4) ln((2/(1+tanu)))du =(π/4)ln(2)−∫_0 ^(π/4) ln(1+tanu)du ⇒ ∫_0 ^(π/4) ln(1+tanθ)dθ =(π/8)ln(2) ⇒ Φ=(π/4)ln(2)−(π/8)ln(2) =(π/8)ln(2)](Q129831.png)
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{arctanx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\mathrm{by}\:\mathrm{parts}\:\Phi=\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)×\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{hsve} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)\mathrm{d}\theta\:\:=_{\theta=\frac{\pi}{\mathrm{4}}−\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{tanu}}{\mathrm{1}+\mathrm{tanu}}\right)\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tanu}}\right)\mathrm{du}\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tanu}\right)\mathrm{du}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)\mathrm{d}\theta\:=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\Phi=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right)\:=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$
