
Question Number 117087 by mnjuly1970 last updated on 09/Oct/20
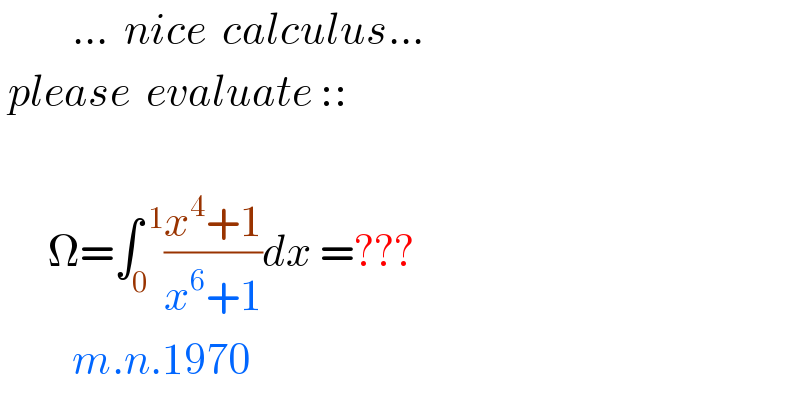
$$\:\:\:\:\:\:\:\:\:...\:\:{nice}\:\:{calculus}... \\ $$$$\:{please}\:\:{evaluate}\::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}\:=??? \\ $$$$\:\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$
Answered by TANMAY PANACEA last updated on 09/Oct/20
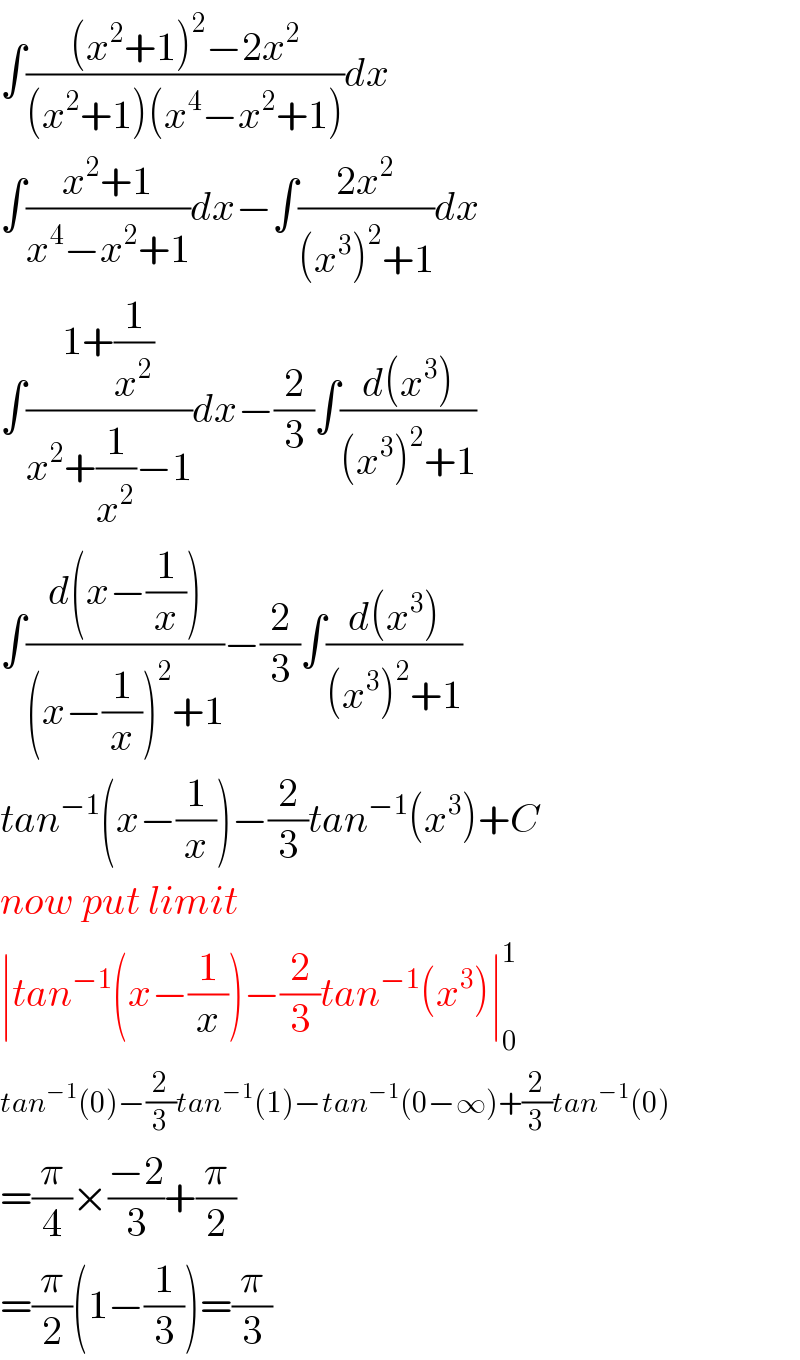
$$\int\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\int\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}{dx}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{d}\left({x}^{\mathrm{3}} \right)}{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{d}\left({x}^{\mathrm{3}} \right)}{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${tan}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({x}^{\mathrm{3}} \right)+{C} \\ $$$${now}\:{put}\:{limit} \\ $$$$\mid{tan}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({x}^{\mathrm{3}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${tan}^{−\mathrm{1}} \left(\mathrm{0}\right)−\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{0}−\infty\right)+\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}×\frac{−\mathrm{2}}{\mathrm{3}}+\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 09/Oct/20
$${thank}\:{you}\:{so}\:{much}\:\:{master}... \\ $$
Commented by TANMAY PANACEA last updated on 09/Oct/20
$${most}\:{welcome}\:{sir} \\ $$
Answered by 1549442205PVT last updated on 09/Oct/20
![((x^4 +1)/(x^6 +1))=((ax+b)/(x^2 +1))+((cx^3 +dx^2 +ex+f)/(x^4 −x^2 +1)) ⇔x^4 +1≡(a+c)^5 +(b+d)x^4 +(c−a+e)x^3 +(f−b+d)x^2 +(a+e)x+b+f ⇔ { ((a+c=0)),((b+d=1)),((b+f=1)),((c−a+e=0)),((f−b+d=0)),((a+e=0)) :}⇔ { ((d=f=1/3)),((b=2/3)),((a=c=e=0)) :} ⇒((x^4 +1)/(x^6 +1))=(2/(3(x^2 +1)))+((x^2 +1)/(3(x^4 −x^2 +1)))(1) ((x^2 +1)/(x^4 −x^2 +1))=((ax+b)/(x^2 +x(√3)+1))+((cx+d)/(x^2 −x(√3)+1)) Similarly,we get a=c=0,b=d=1/2 ⇒((x^2 +1)/(x^4 −x^2 +1))=(1/(2(x^2 +x(√3)+1)))+(1/(2(x^2 −x(√3)+1)))(2) From (1)(2)we get Ω=∫_0 ^( 1) ((x^4 +1)/(x^6 +1))dx=(2/3)∫_0 ^( 1) (dx/(x^2 +1)) +(1/6)∫_0 ^( 1) (dx/(x^2 +x(√3)+1))+(1/6)∫_0 ^( 1) (dx/(x^2 −x(√3)+1)) =(2/3)tan^(−1) (x)∣_0 ^1 +(1/6)∫_0 ^( 1) ((d(x+((√3)/2)))/((x+((√3)/2))^2 +((1/2))^2 )) +(1/6)∫_0 ^( 1) ((d(x−((√3)/2)))/((x−((√3)/2))^2 +((1/2))^2 ))(∫(dx/(x^2 +a^2 ))=(1/a)tan^(−1) ((x/a))) =[(2/3)tan^(−1) (x)+(1/3)tan^(−1) (2x+(√3)) +(1/3)tan^(−1) (2x−(√3))]_0 ^1 =(2/3)×(π/4)+(1/3)×((5π)/(12))+(1/3)×(π/(12))=(π/6)+(π/6) Thus,we obtain Ω=(π/3)](Q117117.png)
$$\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}=\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{cx}^{\mathrm{3}} +\mathrm{dx}^{\mathrm{2}} +\mathrm{ex}+\mathrm{f}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{4}} +\mathrm{1}\equiv\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{5}} +\left(\mathrm{b}+\mathrm{d}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{c}−\mathrm{a}+\mathrm{e}\right)\mathrm{x}^{\mathrm{3}} \\ $$$$+\left(\mathrm{f}−\mathrm{b}+\mathrm{d}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{a}+\mathrm{e}\right)\mathrm{x}+\mathrm{b}+\mathrm{f} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{a}+\mathrm{c}=\mathrm{0}}\\{\mathrm{b}+\mathrm{d}=\mathrm{1}}\\{\mathrm{b}+\mathrm{f}=\mathrm{1}}\\{\mathrm{c}−\mathrm{a}+\mathrm{e}=\mathrm{0}}\\{\mathrm{f}−\mathrm{b}+\mathrm{d}=\mathrm{0}}\\{\mathrm{a}+\mathrm{e}=\mathrm{0}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{d}=\mathrm{f}=\mathrm{1}/\mathrm{3}}\\{\mathrm{b}=\mathrm{2}/\mathrm{3}}\\{\mathrm{a}=\mathrm{c}=\mathrm{e}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}}+\frac{\mathrm{cx}+\mathrm{d}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$$\mathrm{Similarly},\mathrm{we}\:\mathrm{get}\:\mathrm{a}=\mathrm{c}=\mathrm{0},\mathrm{b}=\mathrm{d}=\mathrm{1}/\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}\right)}\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{d}\left(\mathrm{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\left(\mathrm{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{d}\left(\mathrm{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\left(\mathrm{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\left(\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{a}}\right)\right) \\ $$$$=\left[\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}+\sqrt{\mathrm{3}}\right)\right. \\ $$$$\left.+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}−\sqrt{\mathrm{3}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{5}\pi}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{3}}×\frac{\pi}{\mathrm{12}}=\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{6}} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{obtain}}\:\Omega=\frac{\pi}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 09/Oct/20
$${thank}\:{you}\:{so}\:{much} \\ $$$${your}\:{work}\:{is}\:{really} \\ $$$${admirable}. \\ $$
Commented by 1549442205PVT last updated on 10/Oct/20

$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
