
Question Number 141082 by mnjuly1970 last updated on 15/May/21
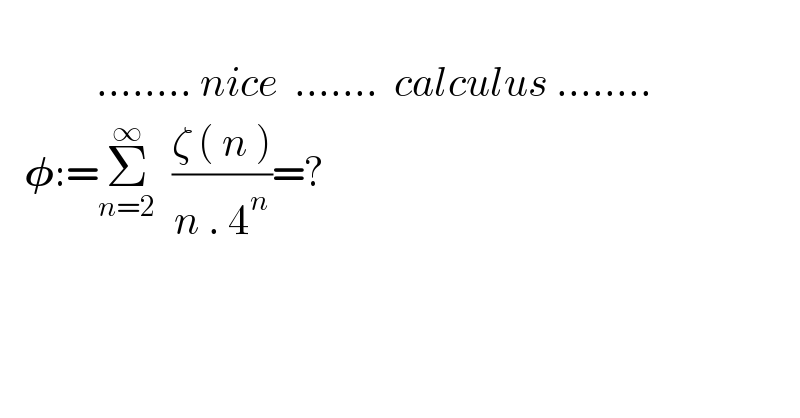
$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:........\:{nice}\:\:.......\:\:{calculus}\:........ \\ $$$$\:\:\:\boldsymbol{\phi}:=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\:\frac{\zeta\:\left(\:{n}\:\right)}{{n}\:.\:\mathrm{4}^{{n}} }=? \\ $$$$ \\ $$
Answered by mindispower last updated on 15/May/21
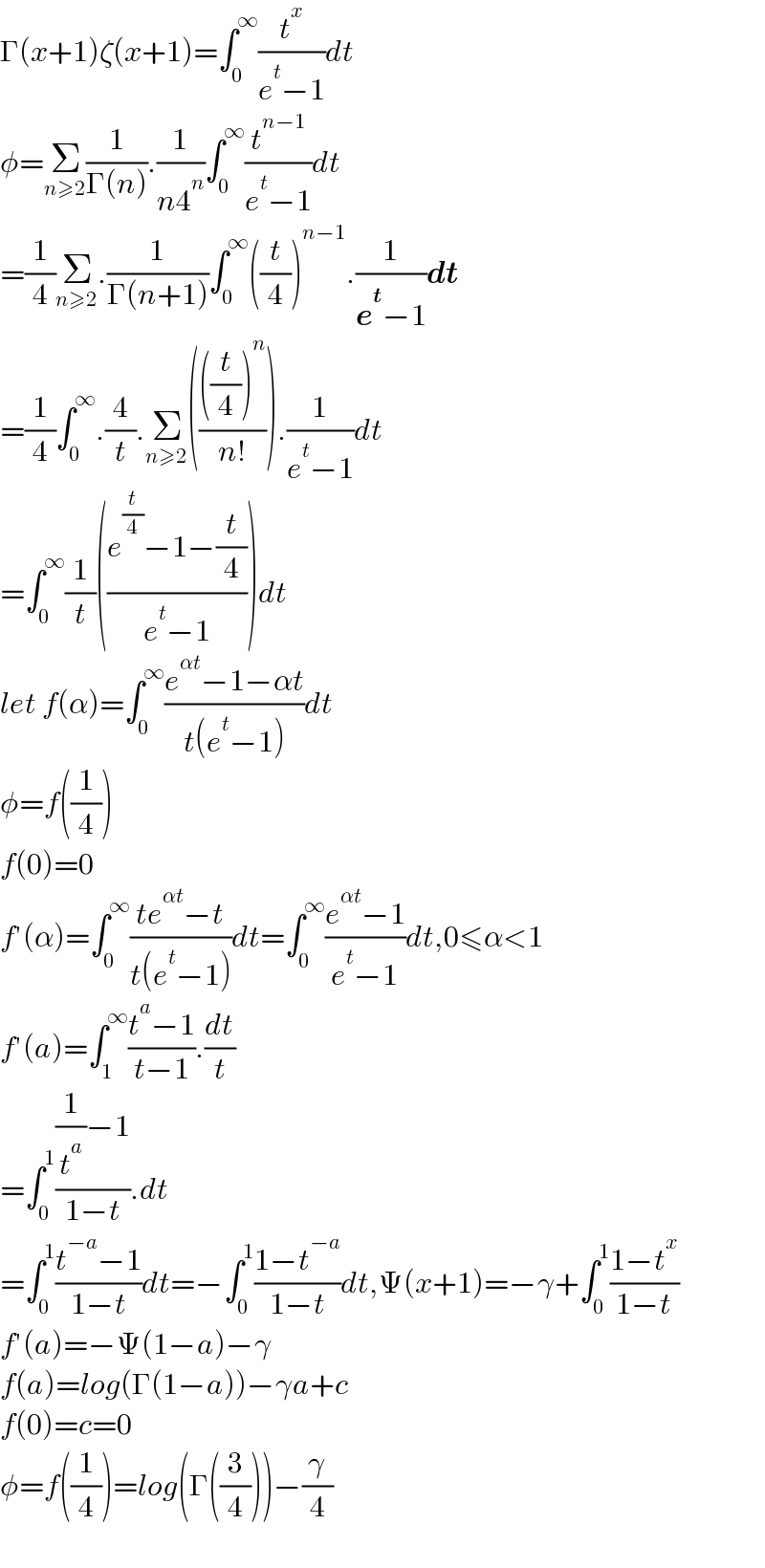
$$\Gamma\left({x}+\mathrm{1}\right)\zeta\left({x}+\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}} }{{e}^{{t}} −\mathrm{1}}{dt} \\ $$$$\phi=\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{\Gamma\left({n}\right)}.\frac{\mathrm{1}}{{n}\mathrm{4}^{{n}} }\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{n}−\mathrm{1}} }{{e}^{{t}} −\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\geqslant\mathrm{2}} {\sum}.\frac{\mathrm{1}}{\Gamma\left({n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} \left(\frac{{t}}{\mathrm{4}}\right)^{{n}−\mathrm{1}} .\frac{\mathrm{1}}{\boldsymbol{{e}}^{\boldsymbol{{t}}} −\mathrm{1}}\boldsymbol{{dt}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} .\frac{\mathrm{4}}{{t}}.\underset{{n}\geqslant\mathrm{2}} {\sum}\left(\frac{\left(\frac{{t}}{\mathrm{4}}\right)^{{n}} }{{n}!}\right).\frac{\mathrm{1}}{{e}^{{t}} −\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{t}}\left(\frac{{e}^{\frac{{t}}{\mathrm{4}}} −\mathrm{1}−\frac{{t}}{\mathrm{4}}}{{e}^{{t}} −\mathrm{1}}\right){dt} \\ $$$${let}\:{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{\alpha{t}} −\mathrm{1}−\alpha{t}}{{t}\left({e}^{{t}} −\mathrm{1}\right)}{dt} \\ $$$$\phi={f}\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{te}^{\alpha{t}} −{t}}{{t}\left({e}^{{t}} −\mathrm{1}\right)}{dt}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{\alpha{t}} −\mathrm{1}}{{e}^{{t}} −\mathrm{1}}{dt},\mathrm{0}\leqslant\alpha<\mathrm{1} \\ $$$${f}'\left({a}\right)=\int_{\mathrm{1}} ^{\infty} \frac{{t}^{{a}} −\mathrm{1}}{{t}−\mathrm{1}}.\frac{{dt}}{{t}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{\mathrm{1}}{{t}^{{a}} }−\mathrm{1}}{\mathrm{1}−{t}}.{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{−{a}} −\mathrm{1}}{\mathrm{1}−{t}}{dt}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{−{a}} }{\mathrm{1}−{t}}{dt},\Psi\left({x}+\mathrm{1}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{{x}} }{\mathrm{1}−{t}} \\ $$$${f}'\left({a}\right)=−\Psi\left(\mathrm{1}−{a}\right)−\gamma \\ $$$${f}\left({a}\right)={log}\left(\Gamma\left(\mathrm{1}−{a}\right)\right)−\gamma{a}+{c} \\ $$$${f}\left(\mathrm{0}\right)={c}=\mathrm{0} \\ $$$$\phi={f}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)={log}\left(\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)−\frac{\gamma}{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 15/May/21
$${bravo}\:{bravo}\:{sir}\:{power}... \\ $$
Commented by mindispower last updated on 15/May/21

$${withe}\:{pleasur}\:{Sir} \\ $$
Answered by mnjuly1970 last updated on 15/May/21
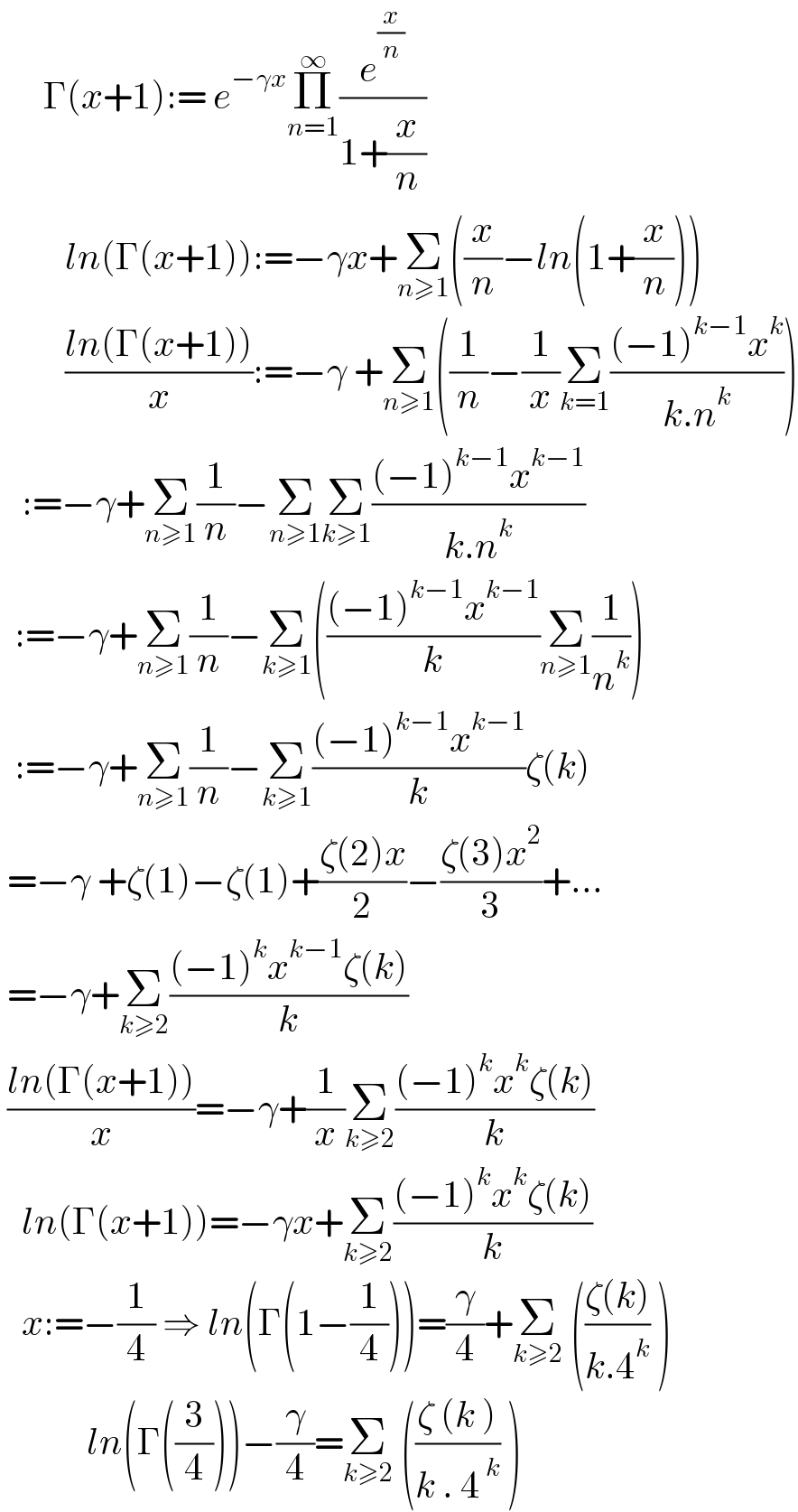
$$\:\:\:\:\:\:\Gamma\left({x}+\mathrm{1}\right):=\:{e}^{−\gamma{x}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{{e}^{\frac{{x}}{{n}}} }{\mathrm{1}+\frac{{x}}{{n}}} \\ $$$$\:\:\:\:\:\:\:\:\:{ln}\left(\Gamma\left({x}+\mathrm{1}\right)\right):=−\gamma{x}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{{x}}{{n}}−{ln}\left(\mathrm{1}+\frac{{x}}{{n}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{ln}\left(\Gamma\left({x}+\mathrm{1}\right)\right)}{{x}}:=−\gamma\:+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{x}}\underset{{k}=\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {x}^{{k}} }{{k}.{n}^{{k}} }\right) \\ $$$$\:\:\::=−\gamma+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}−\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {x}^{{k}−\mathrm{1}} }{{k}.{n}^{{k}} } \\ $$$$\:\::=−\gamma+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}−\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {x}^{{k}−\mathrm{1}} }{{k}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{{k}} }\right) \\ $$$$\:\::=−\gamma+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {x}^{{k}−\mathrm{1}} }{{k}}\zeta\left({k}\right) \\ $$$$\:=−\gamma\:+\zeta\left(\mathrm{1}\right)−\zeta\left(\mathrm{1}\right)+\frac{\zeta\left(\mathrm{2}\right){x}}{\mathrm{2}}−\frac{\zeta\left(\mathrm{3}\right){x}^{\mathrm{2}} }{\mathrm{3}}+... \\ $$$$\:=−\gamma+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{k}−\mathrm{1}} \zeta\left({k}\right)}{{k}} \\ $$$$\:\frac{{ln}\left(\Gamma\left({x}+\mathrm{1}\right)\right)}{{x}}=−\gamma+\frac{\mathrm{1}}{{x}}\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \zeta\left({k}\right)}{{k}} \\ $$$$\:\:\:{ln}\left(\Gamma\left({x}+\mathrm{1}\right)\right)=−\gamma{x}+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \zeta\left({k}\right)}{{k}} \\ $$$$\:\:\:{x}:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{ln}\left(\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\right)=\frac{\gamma}{\mathrm{4}}+\underset{{k}\geqslant\mathrm{2}} {\sum}\:\left(\frac{\zeta\left({k}\right)}{{k}.\mathrm{4}^{{k}} }\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{ln}\left(\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)−\frac{\gamma}{\mathrm{4}}=\underset{{k}\geqslant\mathrm{2}} {\sum}\:\left(\frac{\zeta\:\left({k}\:\right)}{{k}\:.\:\mathrm{4}^{\:{k}} }\:\right) \\ $$
Commented by mindispower last updated on 15/May/21

$${sir}\:{are}\:{you}\:{student}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 15/May/21
![ψ(z+1)=−γ+Σ_(n=2) ^∞ ζ(n)z^(n−1) [log(Γ(z+1))]_0 ^(−(1/4)) =−∫_0 ^((−1)/4) γ+Σ_(n=2) ^∞ ∫_0 ^(−(1/4)) (−1)^n ζ(n)z^(n−1) dz log(Γ((3/4)))=(γ/4)+Σ((ζ(n))/(n4^n )) Σ((ζ(n))/(n4^n ))=log(Γ((3/4)))−(γ/4)](Q141103.png)
$$\psi\left({z}+\mathrm{1}\right)=−\gamma+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\zeta\left({n}\right){z}^{{n}−\mathrm{1}} \\ $$$$\left[{log}\left(\Gamma\left({z}+\mathrm{1}\right)\right)\right]_{\mathrm{0}} ^{−\frac{\mathrm{1}}{\mathrm{4}}} =−\int_{\mathrm{0}} ^{\frac{−\mathrm{1}}{\mathrm{4}}} \gamma+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{−\frac{\mathrm{1}}{\mathrm{4}}} \left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right){z}^{{n}−\mathrm{1}} {dz} \\ $$$${log}\left(\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)=\frac{\gamma}{\mathrm{4}}+\Sigma\frac{\zeta\left({n}\right)}{{n}\mathrm{4}^{{n}} } \\ $$$$\Sigma\frac{\zeta\left({n}\right)}{{n}\mathrm{4}^{{n}} }={log}\left(\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)−\frac{\gamma}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 15/May/21

$$\:{very}\:{very}\:{nice} \\ $$$${thank}\:{you}\:{mr}\:{payan}... \\ $$$$\:{taylor}\:{expansion}\:{of}\:{digamma}.. \\ $$
