
Question Number 117806 by mnjuly1970 last updated on 13/Oct/20
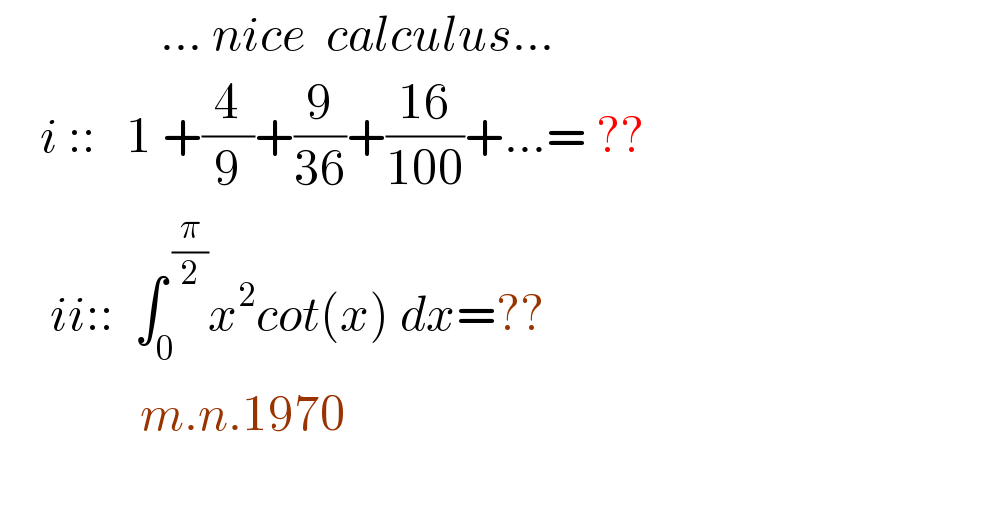
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:{calculus}... \\ $$$$\:\:\:\:{i}\:::\:\:\:\mathrm{1}\:+\frac{\mathrm{4}}{\mathrm{9}}+\frac{\mathrm{9}}{\mathrm{36}}+\frac{\mathrm{16}}{\mathrm{100}}+...=\:?? \\ $$$$\:\:\:\:\:{ii}::\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} {cot}\left({x}\right)\:{dx}=?? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$$$ \\ $$
Commented by TANMAY PANACEA last updated on 13/Oct/20
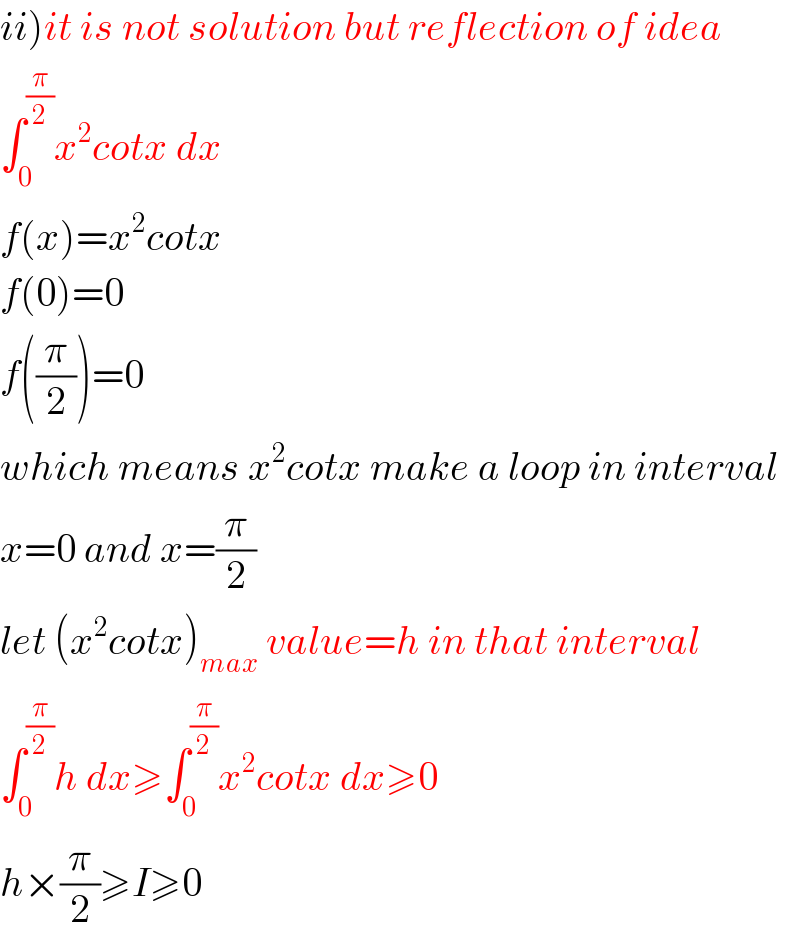
$$\left.{ii}\right){it}\:{is}\:{not}\:{solution}\:{but}\:{reflection}\:{of}\:{idea} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} {cotx}\:{dx} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} {cotx} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${which}\:{means}\:{x}^{\mathrm{2}} {cotx}\:{make}\:{a}\:{loop}\:{in}\:{interval} \\ $$$${x}=\mathrm{0}\:{and}\:{x}=\frac{\pi}{\mathrm{2}} \\ $$$${let}\:\left({x}^{\mathrm{2}} {cotx}\right)_{{max}} \:{value}={h}\:{in}\:{that}\:{interval} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {h}\:{dx}\geqslant\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} {cotx}\:{dx}\geqslant\mathrm{0} \\ $$$${h}×\frac{\pi}{\mathrm{2}}\geqslant{I}\geqslant\mathrm{0} \\ $$
Commented by Lordose last updated on 13/Oct/20
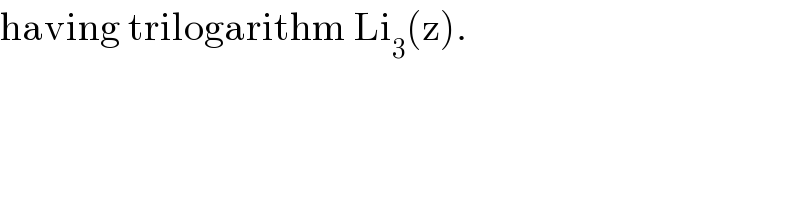
$$\mathrm{having}\:\mathrm{trilogarithm}\:\mathrm{Li}_{\mathrm{3}} \left(\mathrm{z}\right). \\ $$
Answered by Dwaipayan Shikari last updated on 13/Oct/20
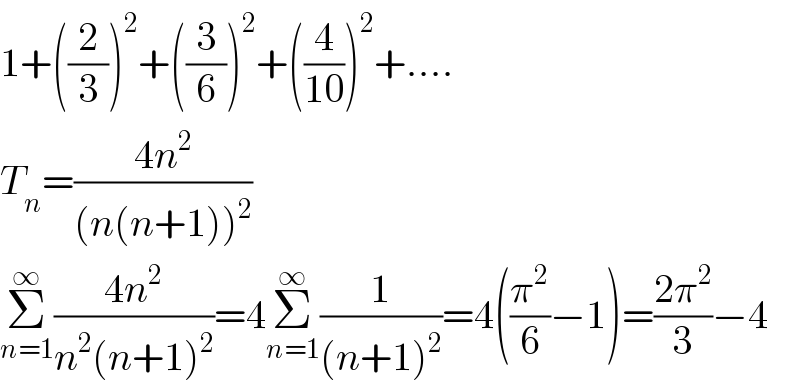
$$\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{6}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{10}}\right)^{\mathrm{2}} +.... \\ $$$${T}_{{n}} =\frac{\mathrm{4}{n}^{\mathrm{2}} }{\left({n}\left({n}+\mathrm{1}\right)\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{4}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}\right)=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{4} \\ $$
Commented by mnjuly1970 last updated on 13/Oct/20
$${mercey}\:{mr}\:{dwaipayan}.. \\ $$
Answered by mnjuly1970 last updated on 13/Oct/20

$$\:\:\: \\ $$
Answered by mindispower last updated on 14/Oct/20
![∫x^2 cot(x) dx =[x^2 ln(sin(x))dx]−∫2xlnsin(x)dx =2∫x(−ln(sin(x))dx byfourier −ln(sin(x))=ln(2)+Σ_(n≥1) ((cos(2nx))/n) we get 2∫_0 ^(π/2) (xln(2)+xΣ_(n≥1) ((cos(2nx))/n))dx =(π^2 /4)ln(2)+2Σ_(n≥1) (1/n)∫_0 ^(π/2) xcos(2nx)dx ∫xcos(2nx)dx=((xsin(2nx))/(2n))+((cos(2nx))/(4n^2 ))+c we get (π^2 /4)ln(2)+2Σ_(n≥1) (1/n)((((−1)^n −1)/(4n^2 ))) =((π^2 ln(2))/4)−Σ_(n≥0) (1/((2n+1)^3 ))=((π^2 ln(2))/4)−(7/8)ζ(3)](Q117906.png)
$$\int{x}^{\mathrm{2}} {cot}\left({x}\right)\:{dx}\:=\left[{x}^{\mathrm{2}} {ln}\left({sin}\left({x}\right)\right){dx}\right]−\int\mathrm{2}{xlnsin}\left({x}\right){dx} \\ $$$$=\mathrm{2}\int{x}\left(−{ln}\left({sin}\left({x}\right)\right){dx}\right. \\ $$$${byfourier}\:−{ln}\left({sin}\left({x}\right)\right)={ln}\left(\mathrm{2}\right)+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$${we}\:{get}\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({xln}\left(\mathrm{2}\right)+{x}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}}\right){dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xcos}\left(\mathrm{2}{nx}\right){dx} \\ $$$$\int{xcos}\left(\mathrm{2}{nx}\right){dx}=\frac{{xsin}\left(\mathrm{2}{nx}\right)}{\mathrm{2}{n}}+\frac{{cos}\left(\mathrm{2}{nx}\right)}{\mathrm{4}{n}^{\mathrm{2}} }+{c}\: \\ $$$${we}\:{get}\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\mathrm{2}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\left(\frac{\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right) \\ $$$$=\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 14/Oct/20

$${very}\:{nice}\:.{thank}\:{you}\:{mr} \\ $$$${power}. \\ $$
Commented by mindispower last updated on 14/Oct/20

$${withe}\:{pleasur}\: \\ $$
Answered by mnjuly1970 last updated on 14/Oct/20
![solution (ii) note:: we know that :: ∫_0 ^( (π/2)) xln(sin(x))dx[=_(ln(sin(x))=−ln(2)−Σ_(n=1) ^∞ ((cos(2nx))/n)) ^(fourier series) ] −ln(2)(π^2 /8)+(7/(16))ζ(3) ✓ therfore:: Ω=∫_0 ^(π/2) x^2 cot(x)dx=^(i.b.p) {x^2 lnsin(x)}_0 ^(π/2) −2∫_0 ^( (π/2)) xln(sin(x))dx =^(note) −2[−ln(2)(π^2 /8)+(7/(16))ζ(3)] =ln(2)(π^2 /4) −(7/8)ζ(3) ✓ ... m.n.1970...](Q117920.png)
$${solution}\:\:\left({ii}\right) \\ $$$$\:\:{note}::\:\:{we}\:{know}\:{that}\:::\: \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {xln}\left({sin}\left({x}\right)\right){dx}\left[\underset{{ln}\left({sin}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}}} {\overset{{fourier}\:{series}} {=}}\right]\:−{ln}\left(\mathrm{2}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{16}}\zeta\left(\mathrm{3}\right)\:\checkmark \\ $$$${therfore}:: \\ $$$$\:\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} {cot}\left({x}\right){dx}\overset{{i}.{b}.{p}} {=}\left\{{x}^{\mathrm{2}} {lnsin}\left({x}\right)\right\}_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {xln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\overset{{note}} {=}−\mathrm{2}\left[−{ln}\left(\mathrm{2}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{16}}\zeta\left(\mathrm{3}\right)\right] \\ $$$$\:\:\:\:\:={ln}\left(\mathrm{2}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:−\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:...\:\:{m}.{n}.\mathrm{1970}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
