
Question Number 138683 by mnjuly1970 last updated on 16/Apr/21
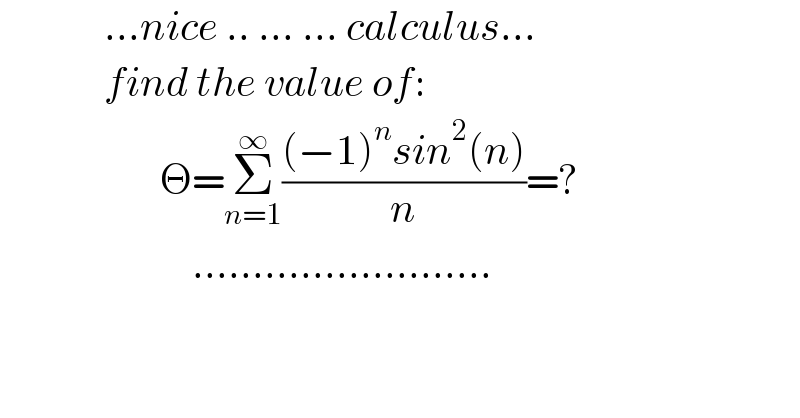
$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:..\:...\:...\:{calculus}... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{find}\:{the}\:{value}\:{of}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Theta=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {sin}^{\mathrm{2}} \left({n}\right)}{{n}}=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......................... \\ $$
Answered by Dwaipayan Shikari last updated on 16/Apr/21
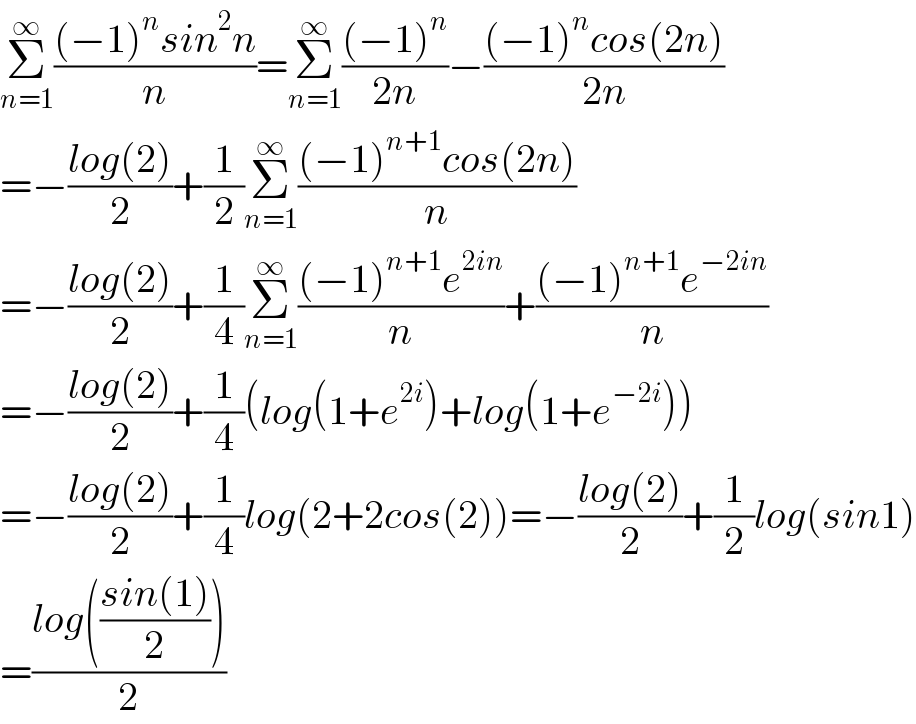
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {sin}^{\mathrm{2}} {n}}{{n}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}}−\frac{\left(−\mathrm{1}\right)^{{n}} {cos}\left(\mathrm{2}{n}\right)}{\mathrm{2}{n}}\:\:\:\:\:\: \\ $$$$=−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {cos}\left(\mathrm{2}{n}\right)}{{n}} \\ $$$$=−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{\mathrm{2}{in}} }{{n}}+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−\mathrm{2}{in}} }{{n}} \\ $$$$=−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\left({log}\left(\mathrm{1}+{e}^{\mathrm{2}{i}} \right)+{log}\left(\mathrm{1}+{e}^{−\mathrm{2}{i}} \right)\right) \\ $$$$=−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}{log}\left(\mathrm{2}+\mathrm{2}{cos}\left(\mathrm{2}\right)\right)=−\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left({sin}\mathrm{1}\right) \\ $$$$=\frac{{log}\left(\frac{{sin}\left(\mathrm{1}\right)}{\mathrm{2}}\right)}{\mathrm{2}} \\ $$
