Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 138223 by mnjuly1970 last updated on 11/Apr/21

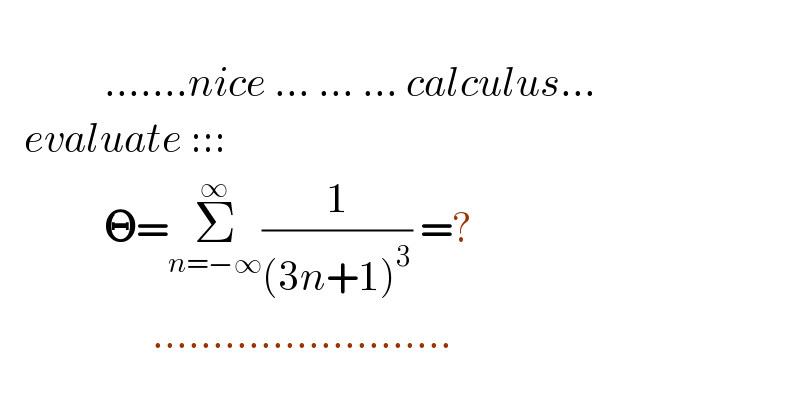
.......nice ... ... ... calculus... evaluate ::: 𝚯=Σ_(n=−∞) ^∞ (1/((3n+1)^3 )) =? .........................

$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:.......{nice}\:...\:...\:...\:{calculus}... \\ $$$$\:\:\:{evaluate}\:::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\Theta}=\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }\:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......................... \\ $$

Answered by Dwaipayan Shikari last updated on 11/Apr/21

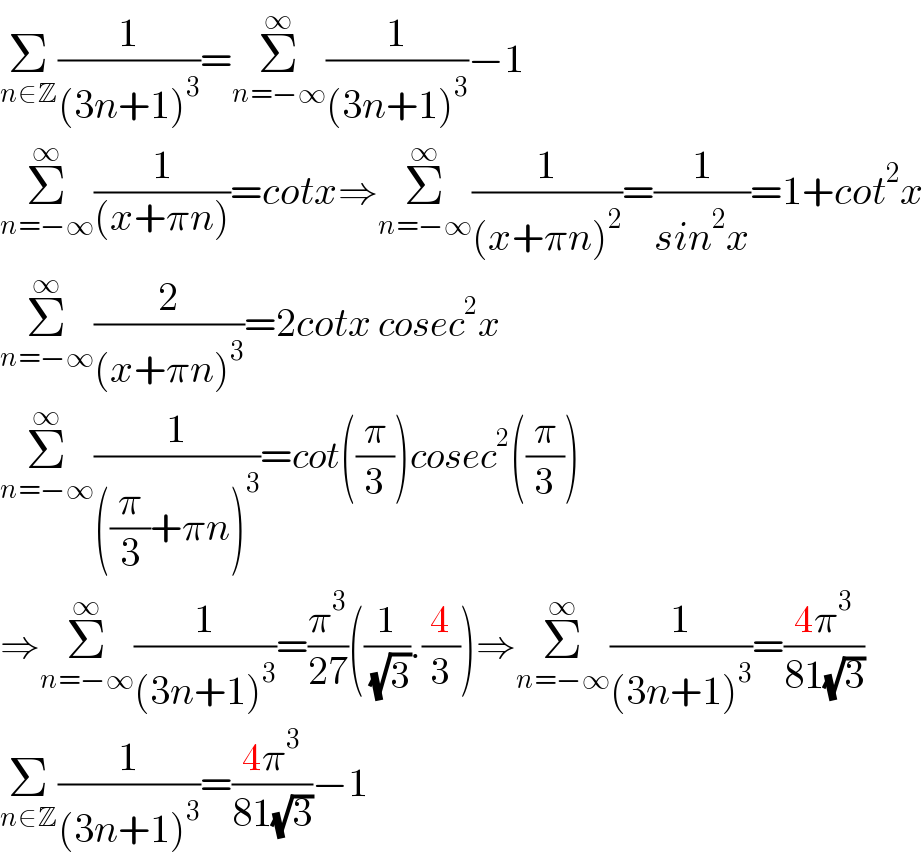
Σ_(n∈Z) (1/((3n+1)^3 ))=Σ_(n=−∞) ^∞ (1/((3n+1)^3 ))−1 Σ_(n=−∞) ^∞ (1/((x+πn)))=cotx⇒Σ_(n=−∞) ^∞ (1/((x+πn)^2 ))=(1/(sin^2 x))=1+cot^2 x Σ_(n=−∞) ^∞ (2/((x+πn)^3 ))=2cotx cosec^2 x Σ_(n=−∞) ^∞ (1/(((π/3)+πn)^3 ))=cot((π/3))cosec^2 ((π/3)) ⇒Σ_(n=−∞) ^∞ (1/((3n+1)^3 ))=(π^3 /(27))((1/( (√3))).(4/3))⇒Σ_(n=−∞) ^∞ (1/((3n+1)^3 ))=((4π^3 )/(81(√3))) Σ_(n∈Z) (1/((3n+1)^3 ))=((4π^3 )/(81(√3)))−1

$$\underset{{n}\in\mathbb{Z}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }−\mathrm{1} \\ $$$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({x}+\pi{n}\right)}={cotx}\Rightarrow\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({x}+\pi{n}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}=\mathrm{1}+{cot}^{\mathrm{2}} {x} \\ $$$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\left({x}+\pi{n}\right)^{\mathrm{3}} }=\mathrm{2}{cotx}\:{cosec}^{\mathrm{2}} {x} \\ $$$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\frac{\pi}{\mathrm{3}}+\pi{n}\right)^{\mathrm{3}} }={cot}\left(\frac{\pi}{\mathrm{3}}\right){cosec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\pi^{\mathrm{3}} }{\mathrm{27}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}.\frac{\mathrm{4}}{\mathrm{3}}\right)\Rightarrow\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{4}\pi^{\mathrm{3}} }{\mathrm{81}\sqrt{\mathrm{3}}}\: \\ $$$$\underset{{n}\in\mathbb{Z}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{4}\pi^{\mathrm{3}} }{\mathrm{81}\sqrt{\mathrm{3}}}−\mathrm{1} \\ $$

Answered by mnjuly1970 last updated on 11/Apr/21

thank you so much...

$$\:{thank}\:{you}\:{so}\:{much}... \\ $$

Commented by Dwaipayan Shikari last updated on 11/Apr/21

Sorry i had a typo . kindly check

$${Sorry}\:{i}\:{had}\:{a}\:{typo}\:.\:{kindly}\:{check} \\ $$

Commented by mnjuly1970 last updated on 11/Apr/21

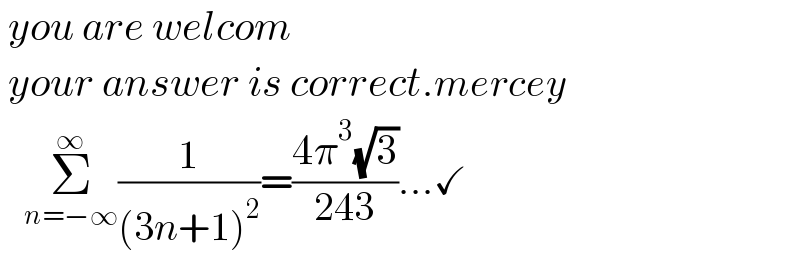
you are welcom your answer is correct.mercey Σ_(n=−∞) ^∞ (1/((3n+1)^2 ))=((4π^3 (√3))/(243))...✓

$$\:{you}\:{are}\:{welcom} \\ $$$$\:{your}\:{answer}\:{is}\:{correct}.{mercey} \\ $$$$\:\:\:\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{4}\pi^{\mathrm{3}} \sqrt{\mathrm{3}}}{\mathrm{243}}...\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com