
Question Number 130198 by mnjuly1970 last updated on 23/Jan/21
![....nice calculus... calculate:: L [e^(−t) . (√(t )) ] =_(transform) ^(Laplace) ? ...](Q130198.png)
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....{nice}\:\:{calculus}... \\ $$$$\:\:\:\:{calculate}:: \\ $$$$\:\:\:\:\:\:\mathscr{L}\:\left[{e}^{−{t}} .\:\sqrt{{t}\:}\:\right]\:\underset{{transform}} {\overset{{Laplace}} {=}}\:?\:... \\ $$$$\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jan/21
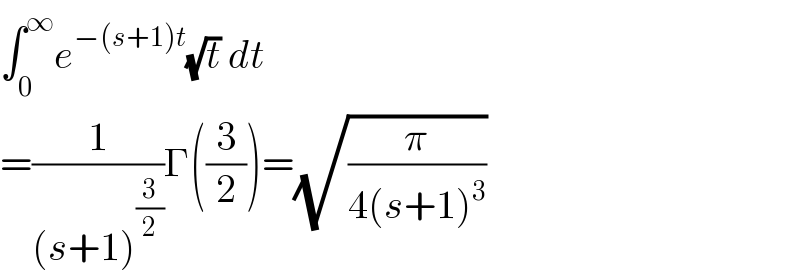
$$\int_{\mathrm{0}} ^{\infty} {e}^{−\left({s}+\mathrm{1}\right){t}} \sqrt{{t}}\:{dt}\:\:\:\:\: \\ $$$$=\frac{\mathrm{1}}{\left({s}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\sqrt{\frac{\pi}{\mathrm{4}\left({s}+\mathrm{1}\right)^{\mathrm{3}} }} \\ $$
Commented by mnjuly1970 last updated on 23/Jan/21

$${thanks}\:{alot}.. \\ $$
