
Question Number 140046 by mnjuly1970 last updated on 03/May/21
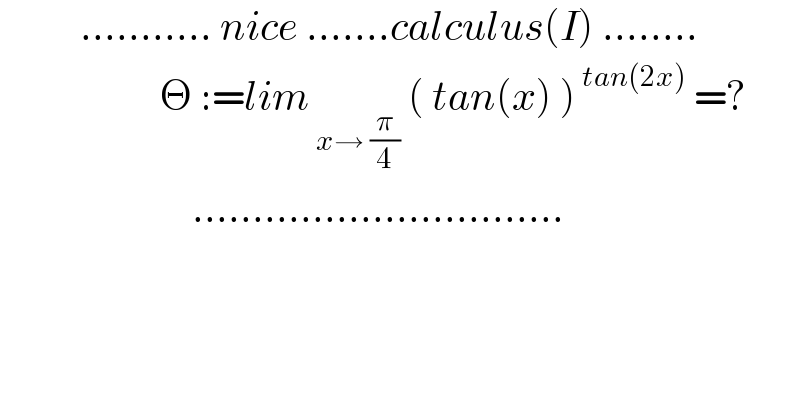
$$\:\:\:\:\:\:\:\:\:\:...........\:{nice}\:.......{calculus}\left({I}\right)\:........ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Theta\::={lim}_{\:{x}\rightarrow\:\frac{\pi}{\mathrm{4}}} \:\left(\:{tan}\left({x}\right)\:\right)^{\:{tan}\left(\mathrm{2}{x}\right)} \:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:............................... \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 03/May/21

$${thanks}\:{alot}... \\ $$
Answered by Dwaipayan Shikari last updated on 03/May/21
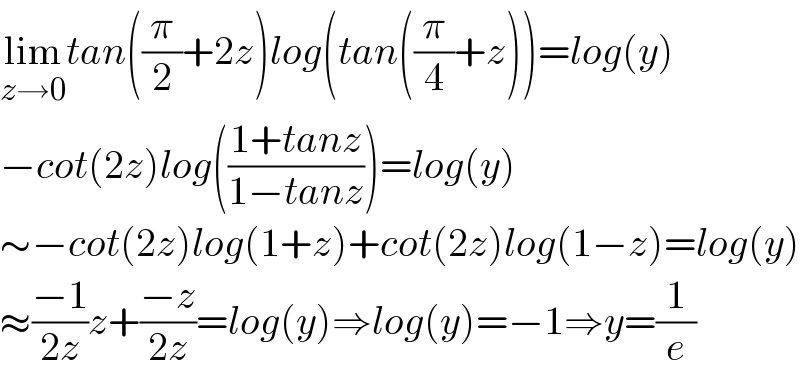
$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}{tan}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{z}\right){log}\left({tan}\left(\frac{\pi}{\mathrm{4}}+{z}\right)\right)={log}\left({y}\right) \\ $$$$−{cot}\left(\mathrm{2}{z}\right){log}\left(\frac{\mathrm{1}+{tanz}}{\mathrm{1}−{tanz}}\right)={log}\left({y}\right) \\ $$$$\sim−{cot}\left(\mathrm{2}{z}\right){log}\left(\mathrm{1}+{z}\right)+{cot}\left(\mathrm{2}{z}\right){log}\left(\mathrm{1}−{z}\right)={log}\left({y}\right) \\ $$$$\approx\frac{−\mathrm{1}}{\mathrm{2}{z}}{z}+\frac{−{z}}{\mathrm{2}{z}}={log}\left({y}\right)\Rightarrow{log}\left({y}\right)=−\mathrm{1}\Rightarrow{y}=\frac{\mathrm{1}}{{e}} \\ $$
Answered by mnjuly1970 last updated on 04/May/21
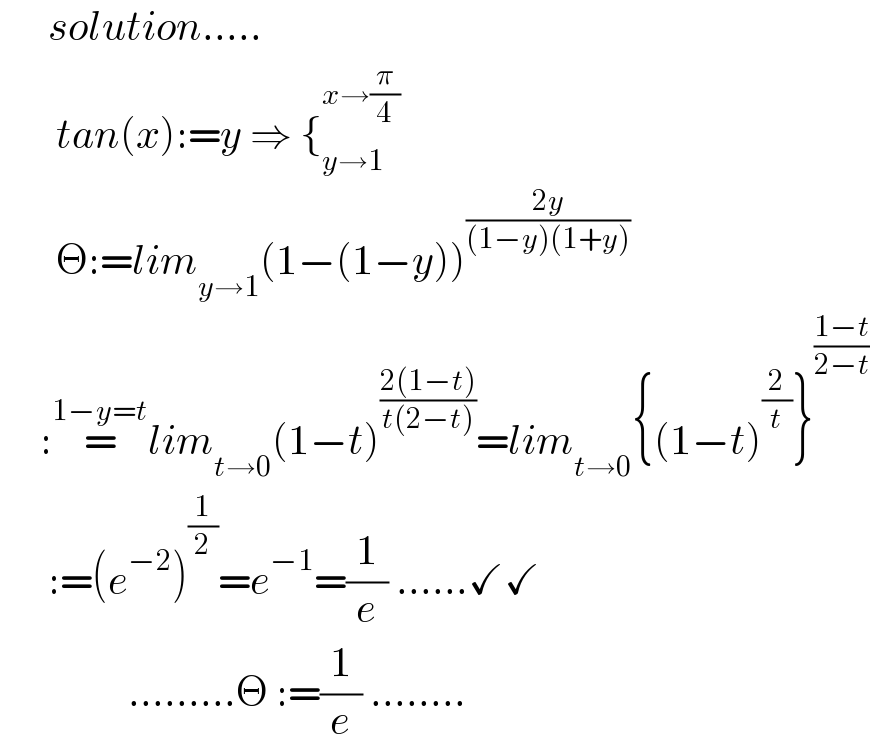
$$\:\:\:\:\:\:{solution}..... \\ $$$$\:\:\:\:\:\:\:{tan}\left({x}\right):={y}\:\Rightarrow\:\left\{_{{y}\rightarrow\mathrm{1}} ^{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \right. \\ $$$$\:\:\:\:\:\:\:\Theta:={lim}_{{y}\rightarrow\mathrm{1}} \left(\mathrm{1}−\left(\mathrm{1}−{y}\right)\right)^{\frac{\mathrm{2}{y}}{\left(\mathrm{1}−{y}\right)\left(\mathrm{1}+{y}\right)}} \\ $$$$\:\:\:\:\::\overset{\mathrm{1}−{y}={t}} {=}{lim}_{{t}\rightarrow\mathrm{0}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{2}\left(\mathrm{1}−{t}\right)}{{t}\left(\mathrm{2}−{t}\right)}} ={lim}_{{t}\rightarrow\mathrm{0}} \left\{\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{2}}{{t}}} \right\}^{\frac{\mathrm{1}−{t}}{\mathrm{2}−{t}}} \\ $$$$\:\:\:\:\:\::=\left({e}^{−\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={e}^{−\mathrm{1}} =\frac{\mathrm{1}}{{e}}\:......\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.........\Theta\::=\frac{\mathrm{1}}{{e}}\:........ \\ $$
