
Question Number 128316 by mnjuly1970 last updated on 08/Jan/21
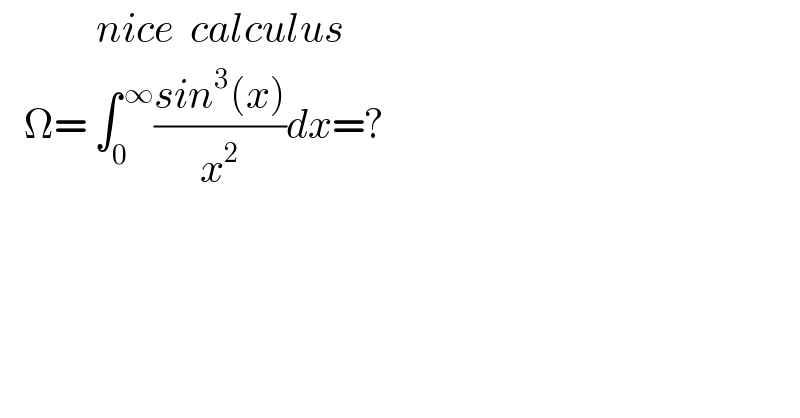
$$\:\:\:\:\:\:\:\:\:\:\:\:{nice}\:\:{calculus} \\ $$$$\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\mathrm{3}} \left({x}\right)}{{x}^{\mathrm{2}} }{dx}=? \\ $$$$ \\ $$
Answered by mindispower last updated on 26/Jan/21
![by part Ω=3∫_0 ^∞ ((cos(x)sin^2 (x))/x)dx =(3/2)∫_0 ^∞ ((sin(2x)sin(x))/x)dx =(3/4)∫_0 ^∞ ((cos(x)−cos(3x))/x)dx =(3/4)Re∫_0 ^∞ ((e^(ix) −e^(3ix) )/x)dx ∫_0 ^∞ ((e^(ix) −e^(3ix) )/x)e^(−xs) dx=f(s),s≥0 f′(s)=∫_0 ^∞ e^(x(i−s)) −e^(x(3i−s) )dx =[(e^(x(i−s)) /(i−s))−(e^(x(3i−s)) /(3i−s))]_0 ^∞ =(1/(s−i))+(1/(3i−s))=f′(s) f(s)=ln(((s−i)/(s−3i)))+c lim_(s→∞) ∫_0 ^∞ ((e^(ix) −e^(3ix) )/x)e^(−xs) dx→0 ⇒c=0 f(0)=ln((1/3))=∫_0 ^∞ ((cos(x)−cos(3x))/x)dx ⇒Ω=−((3ln(3))/4)=(1/4)ln((1/(27)))](Q130510.png)
$${by}\:{part} \\ $$$$\Omega=\mathrm{3}\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({x}\right){sin}^{\mathrm{2}} \left({x}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\mathrm{2}{x}\right){sin}\left({x}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({x}\right)−{cos}\left(\mathrm{3}{x}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}{Re}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{ix}} −{e}^{\mathrm{3}{ix}} }{{x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{ix}} −{e}^{\mathrm{3}{ix}} }{{x}}{e}^{−{xs}} {dx}={f}\left({s}\right),{s}\geqslant\mathrm{0} \\ $$$$\left.{f}'\left({s}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{{x}\left({i}−{s}\right)} −{e}^{{x}\left(\mathrm{3}{i}−{s}\right.} \right){dx} \\ $$$$=\left[\frac{{e}^{{x}\left({i}−{s}\right)} }{{i}−{s}}−\frac{{e}^{{x}\left(\mathrm{3}{i}−{s}\right)} }{\mathrm{3}{i}−{s}}\right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{{s}−{i}}+\frac{\mathrm{1}}{\mathrm{3}{i}−{s}}={f}'\left({s}\right) \\ $$$${f}\left({s}\right)={ln}\left(\frac{{s}−{i}}{{s}−\mathrm{3}{i}}\right)+{c} \\ $$$$\underset{{s}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{ix}} −{e}^{\mathrm{3}{ix}} }{{x}}{e}^{−{xs}} {dx}\rightarrow\mathrm{0} \\ $$$$\Rightarrow{c}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)={ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({x}\right)−{cos}\left(\mathrm{3}{x}\right)}{{x}}{dx} \\ $$$$\Rightarrow\Omega=−\frac{\mathrm{3}{ln}\left(\mathrm{3}\right)}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}}{\mathrm{27}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
