
Question Number 139101 by mnjuly1970 last updated on 22/Apr/21
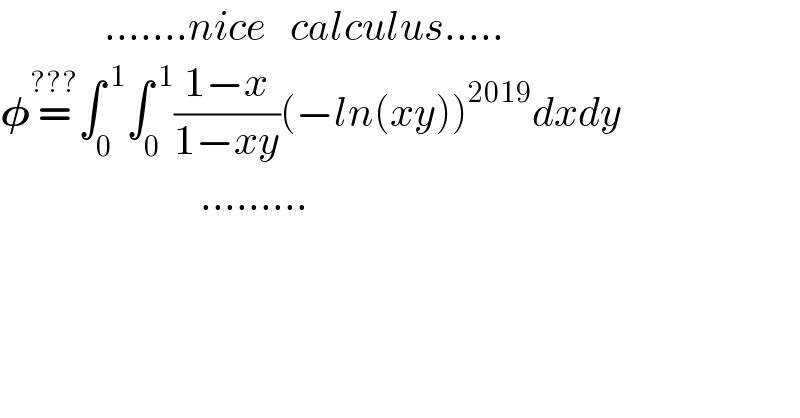
$$\:\:\:\:\:\:\:\:\:\:\:\:\:.......{nice}\:\:\:{calculus}..... \\ $$$$\boldsymbol{\phi}\overset{???} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}−{xy}}\left(−{ln}\left({xy}\right)\right)^{\mathrm{2019}} {dxdy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......... \\ $$
Answered by Dwaipayan Shikari last updated on 22/Apr/21
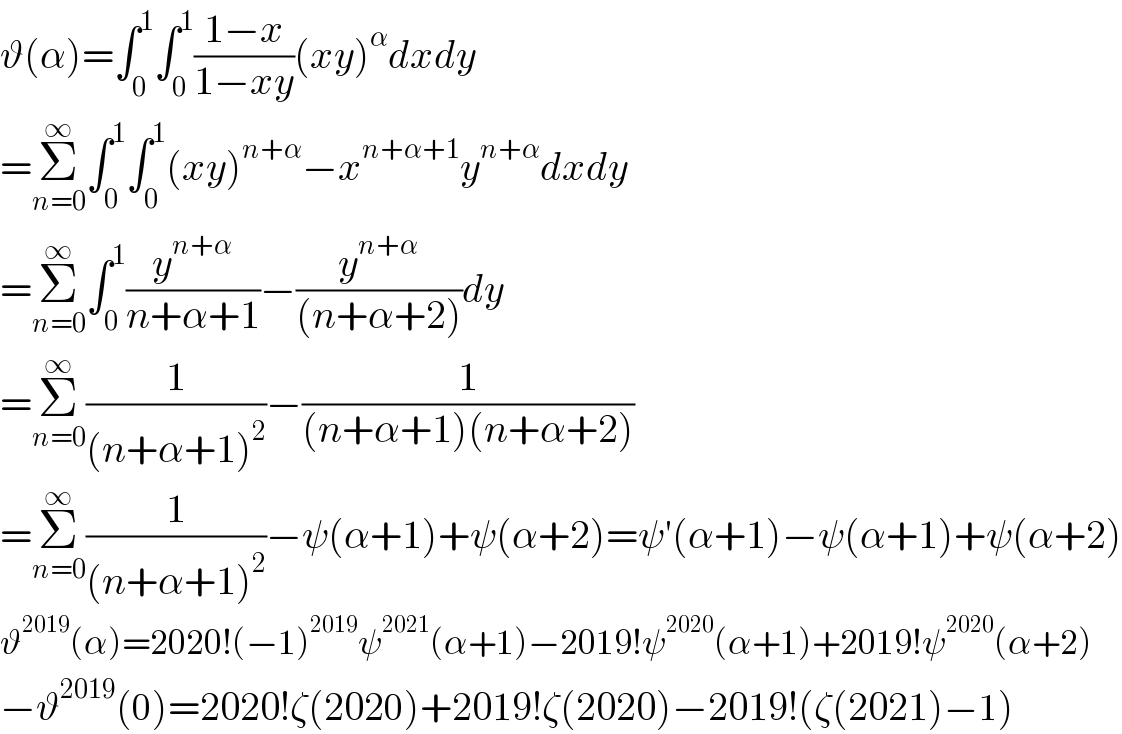
$$\vartheta\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}−{xy}}\left({xy}\right)^{\alpha} {dxdy} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left({xy}\right)^{{n}+\alpha} −{x}^{{n}+\alpha+\mathrm{1}} {y}^{{n}+\alpha} {dxdy} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{y}^{{n}+\alpha} }{{n}+\alpha+\mathrm{1}}−\frac{{y}^{{n}+\alpha} }{\left({n}+\alpha+\mathrm{2}\right)}{dy} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\alpha+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({n}+\alpha+\mathrm{1}\right)\left({n}+\alpha+\mathrm{2}\right)} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\alpha+\mathrm{1}\right)^{\mathrm{2}} }−\psi\left(\alpha+\mathrm{1}\right)+\psi\left(\alpha+\mathrm{2}\right)=\psi'\left(\alpha+\mathrm{1}\right)−\psi\left(\alpha+\mathrm{1}\right)+\psi\left(\alpha+\mathrm{2}\right) \\ $$$$\vartheta^{\mathrm{2019}} \left(\alpha\right)=\mathrm{2020}!\left(−\mathrm{1}\right)^{\mathrm{2019}} \psi^{\mathrm{2021}} \left(\alpha+\mathrm{1}\right)−\mathrm{2019}!\psi^{\mathrm{2020}} \left(\alpha+\mathrm{1}\right)+\mathrm{2019}!\psi^{\mathrm{2020}} \left(\alpha+\mathrm{2}\right) \\ $$$$−\vartheta^{\mathrm{2019}} \left(\mathrm{0}\right)=\mathrm{2020}!\zeta\left(\mathrm{2020}\right)+\mathrm{2019}!\zeta\left(\mathrm{2020}\right)−\mathrm{2019}!\left(\zeta\left(\mathrm{2021}\right)−\mathrm{1}\right) \\ $$
Commented by mnjuly1970 last updated on 22/Apr/21

$$\:\:\:{thanks}\:{alot} \\ $$
