
Question Number 161687 by SANOGO last updated on 21/Dec/21
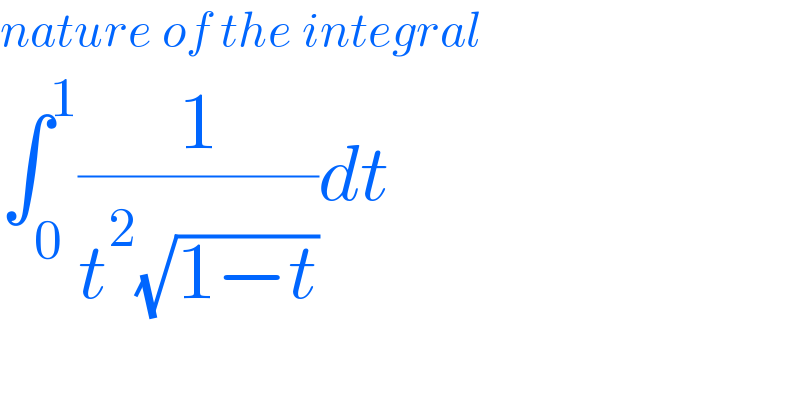
$${nature}\:{of}\:{the}\:{integral} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}}}{dt} \\ $$
Answered by Ar Brandon last updated on 21/Dec/21
![∫_0 ^1 (1/(t^2 (√(1−t))))dt, u=(1/t)⇒−du=(1/t^2 )dt =∫_1 ^∞ (du/( (√(1−(1/u^2 )))))=∫_1 ^∞ (u/( (√(u^2 −1))))du =[(√(u^2 −1))]_1 ^∞ →+∞ divergent](Q161688.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}}}{dt},\:{u}=\frac{\mathrm{1}}{{t}}\Rightarrow−{du}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{du}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}}=\int_{\mathrm{1}} ^{\infty} \frac{{u}}{\:\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}}{du} \\ $$$$=\left[\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\right]_{\mathrm{1}} ^{\infty} \rightarrow+\infty\:\mathrm{divergent} \\ $$
Commented by SANOGO last updated on 22/Dec/21

$${merci}\:{bie}\overset{} {{n}} \\ $$
