
Question Number 162231 by SANOGO last updated on 27/Dec/21
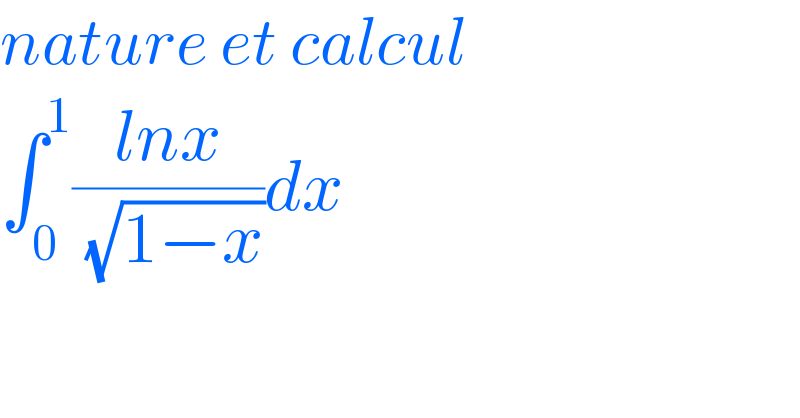
$${nature}\:{et}\:{calcul} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnx}}{\:\sqrt{\mathrm{1}−{x}}}{dx} \\ $$
Answered by amin96 last updated on 27/Dec/21
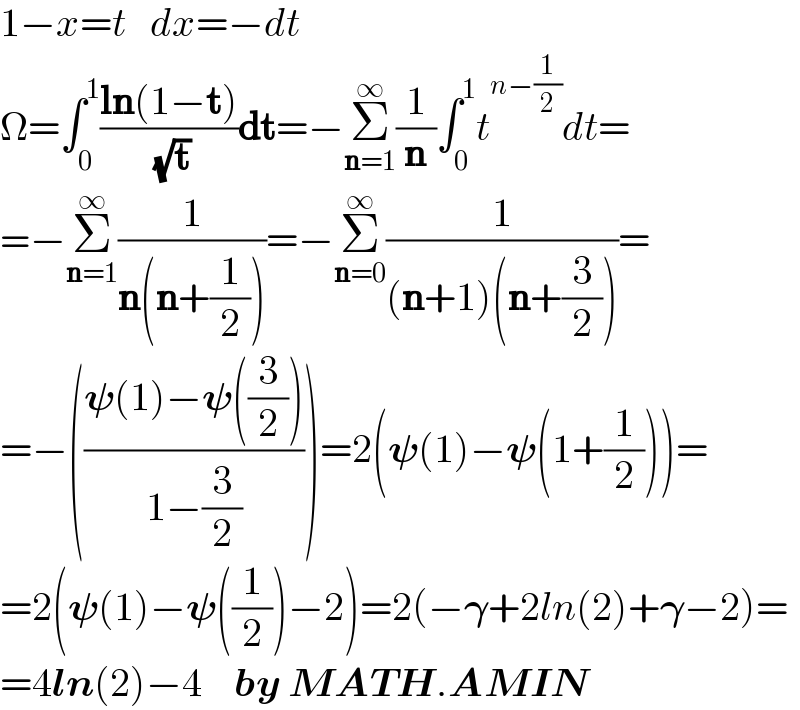
$$\mathrm{1}−{x}={t}\:\:\:{dx}=−{dt} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{t}}\right)}{\:\sqrt{\boldsymbol{\mathrm{t}}}}\boldsymbol{\mathrm{dt}}=−\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} {dt}= \\ $$$$=−\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=−\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{3}}{\mathrm{2}}\right)}= \\ $$$$=−\left(\frac{\boldsymbol{\psi}\left(\mathrm{1}\right)−\boldsymbol{\psi}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}}\right)=\mathrm{2}\left(\boldsymbol{\psi}\left(\mathrm{1}\right)−\boldsymbol{\psi}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)= \\ $$$$=\mathrm{2}\left(\boldsymbol{\psi}\left(\mathrm{1}\right)−\boldsymbol{\psi}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\right)=\mathrm{2}\left(−\boldsymbol{\gamma}+\mathrm{2}{ln}\left(\mathrm{2}\right)+\boldsymbol{\gamma}−\mathrm{2}\right)= \\ $$$$=\mathrm{4}\boldsymbol{{ln}}\left(\mathrm{2}\right)−\mathrm{4}\:\:\:\:\boldsymbol{{by}}\:\boldsymbol{{MATH}}.\boldsymbol{{AMIN}} \\ $$
Commented by SANOGO last updated on 27/Dec/21
$${merci}\:{bien} \\ $$
