Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 199170 by tri26112004 last updated on 28/Oct/23

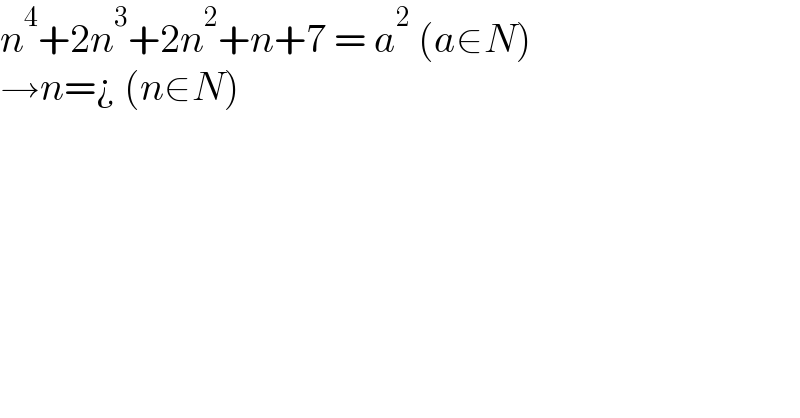
n^4 +2n^3 +2n^2 +n+7 = a^2 (a∈N) →n=¿ (n∈N)

$${n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}\:=\:{a}^{\mathrm{2}} \:\left({a}\in{N}\right) \\ $$$$\rightarrow{n}=¿\:\left({n}\in{N}\right) \\ $$

Commented by Rasheed.Sindhi last updated on 31/Oct/23

Great! ThanX Sir

$$\mathbb{G}\boldsymbol{\mathrm{reat}}! \\ $$$$\:\mathcal{T}{han}\mathcal{X}\:\mathcal{S}{ir}\: \\ $$

Commented by Rasheed.Sindhi last updated on 30/Oct/23

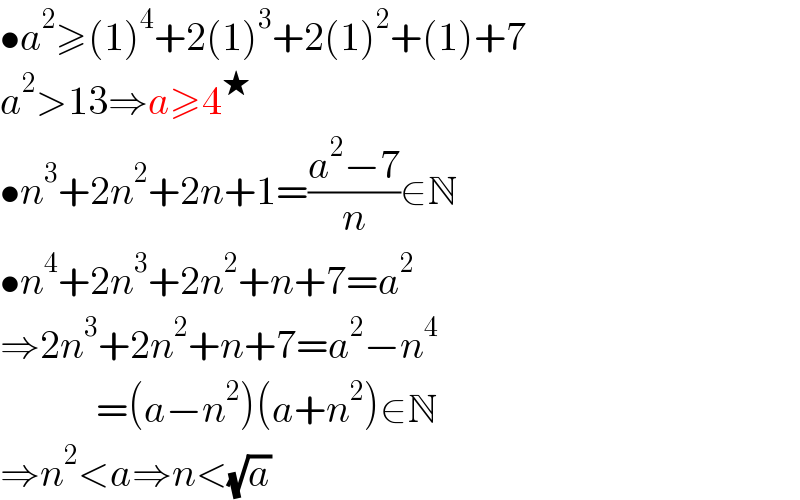
•a^2 ≥(1)^4 +2(1)^3 +2(1)^2 +(1)+7 a^2 >13⇒a≥4^★ •n^3 +2n^2 +2n+1=((a^2 −7)/n)∈N •n^4 +2n^3 +2n^2 +n+7=a^2 ⇒2n^3 +2n^2 +n+7=a^2 −n^4 =(a−n^2 )(a+n^2 )∈N ⇒n^2 <a⇒n<(√a)

$$\bullet{a}^{\mathrm{2}} \geqslant\left(\mathrm{1}\right)^{\mathrm{4}} +\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{3}} +\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}\right)+\mathrm{7} \\ $$$${a}^{\mathrm{2}} >\mathrm{13}\Rightarrow{a}\geqslant\mathrm{4}^{\bigstar} \\ $$$$\bullet{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}=\frac{{a}^{\mathrm{2}} −\mathrm{7}}{{n}}\in\mathbb{N} \\ $$$$\bullet{n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}={a}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}={a}^{\mathrm{2}} −{n}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}−{n}^{\mathrm{2}} \right)\left({a}+{n}^{\mathrm{2}} \right)\in\mathbb{N} \\ $$$$\Rightarrow{n}^{\mathrm{2}} <{a}\Rightarrow{n}<\sqrt{{a}}\: \\ $$

Commented by Rasheed.Sindhi last updated on 30/Oct/23

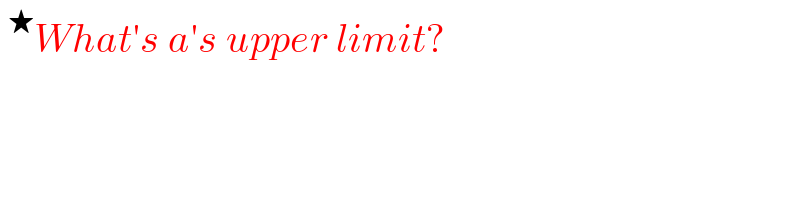
^★ What′s a′s upper limit?

$$\:^{\bigstar} {What}'{s}\:{a}'{s}\:{upper}\:{limit}? \\ $$

Commented by Frix last updated on 30/Oct/23

SOLUTION Part 1 We can factorize it. n^4 +2n^3 +2n^3 +n−a^2 +7=0 n=t−(1/2) t^4 +(t^2 /2)−a^2 +((109)/(16))=0 It′s easy to get n=−(1/2)±((√(−1±2(√(4a^2 −27))))/2) [_(of the ± signs) ^(all 4 combinations) ] n∈R^+ ⇒ n=−(1/2)+((√(−1+2(√(4a^2 −27))))/2) ⇒ for a∈R 4a^2 −27≥0∧−1+2(√(4a^2 −27))≥0 ⇒ a≤−((√(109))/4)∨a≥((√(109))/4) a∈N ⇒ a≥3 No upper limit.

$$\mathbb{SOLUTION}\:\mathrm{Part}\:\mathrm{1} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{factorize}\:\mathrm{it}. \\ $$$${n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{3}} +{n}−{a}^{\mathrm{2}} +\mathrm{7}=\mathrm{0} \\ $$$${n}={t}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}^{\mathrm{4}} +\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−{a}^{\mathrm{2}} +\frac{\mathrm{109}}{\mathrm{16}}=\mathrm{0} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{get} \\ $$$${n}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{1}\pm\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{27}}}}{\mathrm{2}}\:\left[_{\mathrm{of}\:\mathrm{the}\:\pm\:\mathrm{signs}} ^{\mathrm{all}\:\mathrm{4}\:\mathrm{combinations}} \right] \\ $$$${n}\in\mathbb{R}^{+} \:\Rightarrow\:{n}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{27}}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{for}\:{a}\in\mathbb{R} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{27}\geqslant\mathrm{0}\wedge−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{27}}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{a}\leqslant−\frac{\sqrt{\mathrm{109}}}{\mathrm{4}}\vee{a}\geqslant\frac{\sqrt{\mathrm{109}}}{\mathrm{4}} \\ $$$${a}\in\mathbb{N}\:\Rightarrow\:{a}\geqslant\mathrm{3} \\ $$$$\mathrm{No}\:\mathrm{upper}\:\mathrm{limit}. \\ $$

Commented by Rasheed.Sindhi last updated on 30/Oct/23

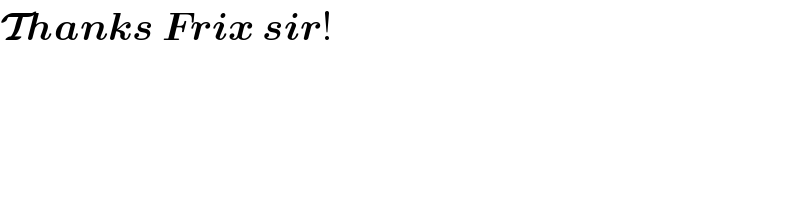
Thanks Frix sir!

$$\boldsymbol{\mathcal{T}{hanks}}\:\boldsymbol{{Frix}}\:\boldsymbol{{sir}}! \\ $$

Commented by Frix last updated on 30/Oct/23

SOLUTION Part 2 4a^2 −27=b^2 4a^2 −b^2 =27 (2a−b)(2a+b)=27 2a−b=1∧2a+b=27 ⇒ a=7∧b=13 ⇒ n=2 ★ 2a−b=3∧2a+b=9 ⇒ a=3∧b=3 ⇒ n∉N No other possibilities.

$$\mathbb{SOLUTION}\:\mathrm{Part}\:\mathrm{2} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{27}={b}^{\mathrm{2}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{27} \\ $$$$\left(\mathrm{2}{a}−{b}\right)\left(\mathrm{2}{a}+{b}\right)=\mathrm{27} \\ $$$$\mathrm{2}{a}−{b}=\mathrm{1}\wedge\mathrm{2}{a}+{b}=\mathrm{27}\:\Rightarrow\:{a}=\mathrm{7}\wedge{b}=\mathrm{13}\:\Rightarrow\:{n}=\mathrm{2}\:\bigstar \\ $$$$\mathrm{2}{a}−{b}=\mathrm{3}\wedge\mathrm{2}{a}+{b}=\mathrm{9}\:\Rightarrow\:{a}=\mathrm{3}\wedge{b}=\mathrm{3}\:\Rightarrow\:{n}\notin\mathbb{N} \\ $$$$\mathrm{No}\:\mathrm{other}\:\mathrm{possibilities}. \\ $$

Commented by Frix last updated on 30/Oct/23

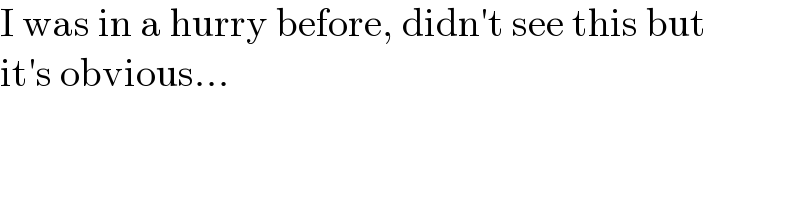
I was in a hurry before, didn′t see this but it′s obvious...

$$\mathrm{I}\:\mathrm{was}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry}\:\mathrm{before},\:\mathrm{didn}'\mathrm{t}\:\mathrm{see}\:\mathrm{this}\:\mathrm{but} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{obvious}... \\ $$

Commented by Frix last updated on 31/Oct/23

��

Commented by tri26112004 last updated on 01/Nov/23

a≥4 and n<(√a) It′s not OK

$${a}\geqslant\mathrm{4}\:{and}\:{n}<\sqrt{{a}} \\ $$$${It}'{s}\:{not}\:{OK} \\ $$

Answered by Frix last updated on 28/Oct/23

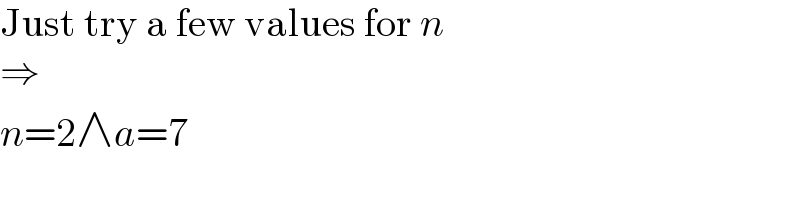
Just try a few values for n ⇒ n=2∧a=7

$$\mathrm{Just}\:\mathrm{try}\:\mathrm{a}\:\mathrm{few}\:\mathrm{values}\:\mathrm{for}\:{n} \\ $$$$\Rightarrow \\ $$$${n}=\mathrm{2}\wedge{a}=\mathrm{7} \\ $$

Commented by tri26112004 last updated on 29/Oct/23

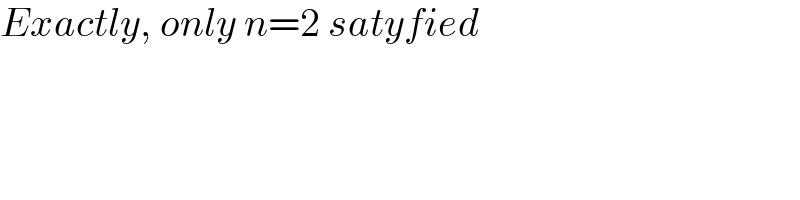
Exactly, only n=2 satyfied

$${Exactly},\:{only}\:{n}=\mathrm{2}\:{satyfied} \\ $$

Answered by Rasheed.Sindhi last updated on 29/Oct/23

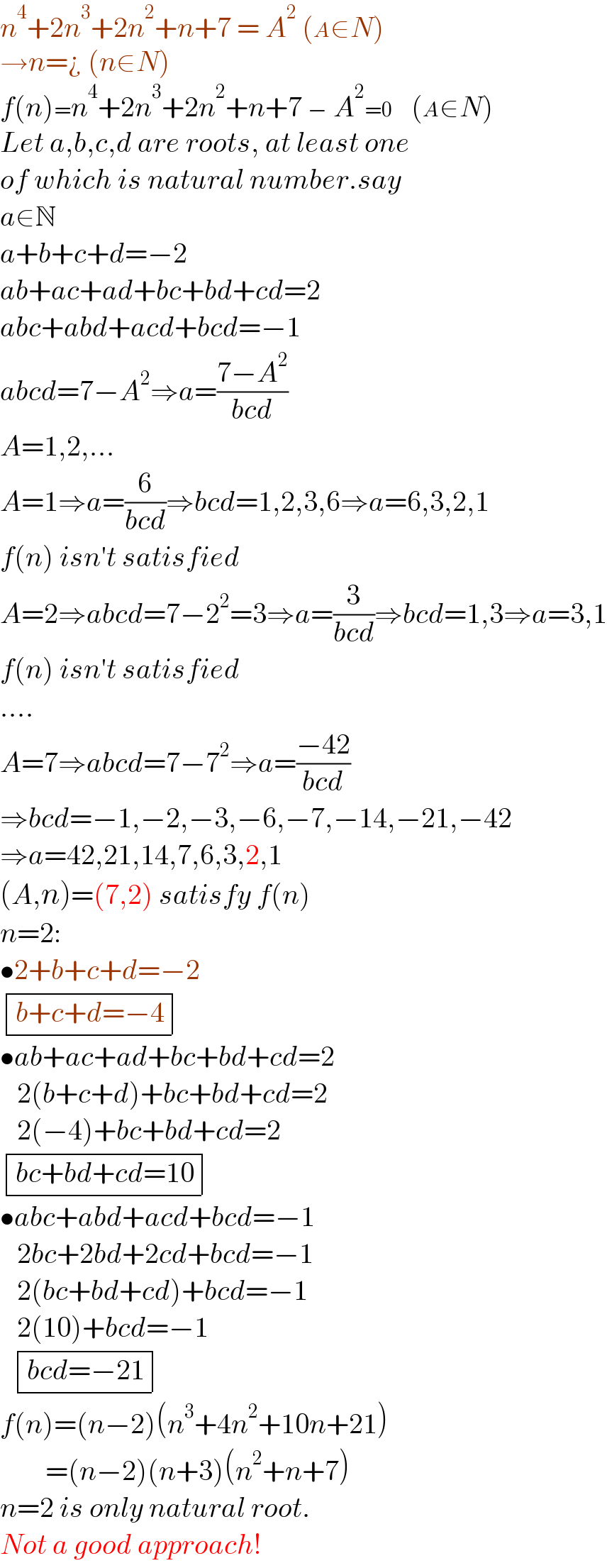
n^4 +2n^3 +2n^2 +n+7 = A^2 (A∈N) →n=¿ (n∈N) f(n)=n^4 +2n^3 +2n^2 +n+7 − A^2 =0 (A∈N) Let a,b,c,d are roots, at least one of which is natural number.say a∈N a+b+c+d=−2 ab+ac+ad+bc+bd+cd=2 abc+abd+acd+bcd=−1 abcd=7−A^2 ⇒a=((7−A^2 )/(bcd)) A=1,2,... A=1⇒a=(6/(bcd))⇒bcd=1,2,3,6⇒a=6,3,2,1 f(n) isn′t satisfied A=2⇒abcd=7−2^2 =3⇒a=(3/(bcd))⇒bcd=1,3⇒a=3,1 f(n) isn′t satisfied .... A=7⇒abcd=7−7^2 ⇒a=((−42)/(bcd)) ⇒bcd=−1,−2,−3,−6,−7,−14,−21,−42 ⇒a=42,21,14,7,6,3,2,1 (A,n)=(7,2) satisfy f(n) n=2: •2+b+c+d=−2 determinant (((b+c+d=−4))) •ab+ac+ad+bc+bd+cd=2 2(b+c+d)+bc+bd+cd=2 2(−4)+bc+bd+cd=2 determinant (((bc+bd+cd=10))) •abc+abd+acd+bcd=−1 2bc+2bd+2cd+bcd=−1 2(bc+bd+cd)+bcd=−1 2(10)+bcd=−1 determinant (((bcd=−21))) f(n)=(n−2)(n^3 +4n^2 +10n+21) =(n−2)(n+3)(n^2 +n+7) n=2 is only natural root. Not a good approach!

$${n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}\:=\:{A}^{\mathrm{2}} \:\left({A}\in{N}\right) \\ $$$$\rightarrow{n}=¿\:\left({n}\in{N}\right) \\ $$$${f}\left({n}\right)={n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}\:−\:{A}^{\mathrm{2}} =\mathrm{0}\:\:\:\:\left({A}\in{N}\right) \\ $$$${Let}\:{a},{b},{c},{d}\:{are}\:{roots},\:{at}\:{least}\:{one} \\ $$$${of}\:{which}\:{is}\:{natural}\:{number}.{say} \\ $$$${a}\in\mathbb{N} \\ $$$${a}+{b}+{c}+{d}=−\mathrm{2}\: \\ $$$${ab}+{ac}+{ad}+{bc}+{bd}+{cd}=\mathrm{2} \\ $$$${abc}+{abd}+{acd}+{bcd}=−\mathrm{1} \\ $$$${abcd}=\mathrm{7}−{A}^{\mathrm{2}} \Rightarrow{a}=\frac{\mathrm{7}−{A}^{\mathrm{2}} }{{bcd}} \\ $$$${A}=\mathrm{1},\mathrm{2},... \\ $$$${A}=\mathrm{1}\Rightarrow{a}=\frac{\mathrm{6}}{{bcd}}\Rightarrow{bcd}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{6}\Rightarrow{a}=\mathrm{6},\mathrm{3},\mathrm{2},\mathrm{1}\: \\ $$$${f}\left({n}\right)\:{isn}'{t}\:{satisfied} \\ $$$${A}=\mathrm{2}\Rightarrow{abcd}=\mathrm{7}−\mathrm{2}^{\mathrm{2}} =\mathrm{3}\Rightarrow{a}=\frac{\mathrm{3}}{{bcd}}\Rightarrow{bcd}=\mathrm{1},\mathrm{3}\Rightarrow{a}=\mathrm{3},\mathrm{1} \\ $$$${f}\left({n}\right)\:{isn}'{t}\:{satisfied} \\ $$$$.... \\ $$$${A}=\mathrm{7}\Rightarrow{abcd}=\mathrm{7}−\mathrm{7}^{\mathrm{2}} \Rightarrow{a}=\frac{−\mathrm{42}}{{bcd}}\: \\ $$$$\Rightarrow{bcd}=−\mathrm{1},−\mathrm{2},−\mathrm{3},−\mathrm{6},−\mathrm{7},−\mathrm{14},−\mathrm{21},−\mathrm{42} \\ $$$$\Rightarrow{a}=\mathrm{42},\mathrm{21},\mathrm{14},\mathrm{7},\mathrm{6},\mathrm{3},\mathrm{2},\mathrm{1} \\ $$$$\left({A},{n}\right)=\left(\mathrm{7},\mathrm{2}\right)\:{satisfy}\:{f}\left({n}\right) \\ $$$${n}=\mathrm{2}: \\ $$$$\bullet\mathrm{2}+{b}+{c}+{d}=−\mathrm{2} \\ $$$$\begin{array}{|c|}{{b}+{c}+{d}=−\mathrm{4}}\\\hline\end{array} \\ $$$$\bullet{ab}+{ac}+{ad}+{bc}+{bd}+{cd}=\mathrm{2} \\ $$$$\:\:\:\mathrm{2}\left({b}+{c}+{d}\right)+{bc}+{bd}+{cd}=\mathrm{2} \\ $$$$\:\:\:\mathrm{2}\left(−\mathrm{4}\right)+{bc}+{bd}+{cd}=\mathrm{2} \\ $$$$\begin{array}{|c|}{{bc}+{bd}+{cd}=\mathrm{10}}\\\hline\end{array} \\ $$$$\bullet{abc}+{abd}+{acd}+{bcd}=−\mathrm{1} \\ $$$$\:\:\:\mathrm{2}{bc}+\mathrm{2}{bd}+\mathrm{2}{cd}+{bcd}=−\mathrm{1} \\ $$$$\:\:\:\mathrm{2}\left({bc}+{bd}+{cd}\right)+{bcd}=−\mathrm{1} \\ $$$$\:\:\:\mathrm{2}\left(\mathrm{10}\right)+{bcd}=−\mathrm{1} \\ $$$$\:\:\begin{array}{|c|}{{bcd}=−\mathrm{21}}\\\hline\end{array} \\ $$$${f}\left({n}\right)=\left({n}−\mathrm{2}\right)\left({n}^{\mathrm{3}} +\mathrm{4}{n}^{\mathrm{2}} +\mathrm{10}{n}+\mathrm{21}\right) \\ $$$$\:\:\:\:\:\:\:\:=\left({n}−\mathrm{2}\right)\left({n}+\mathrm{3}\right)\left({n}^{\mathrm{2}} +{n}+\mathrm{7}\right) \\ $$$${n}=\mathrm{2}\:{is}\:{only}\:{natural}\:{root}. \\ $$$${Not}\:{a}\:{good}\:{approach}! \\ $$

Commented by Rasheed.Sindhi last updated on 29/Oct/23

Once we found n=2 ∧ A=7 We′ve to prove that there′s no other natural root of f(n). For this put A=7 in f(n) and then trying to solve f(n) whose one factor is already known: n−2 n^4 +2n^3 +2n^2 +n+7 − A^2 =0 (A∈N) n^4 +2n^3 +2n^2 +n+7 − 7^2 =0 n^4 +2n^3 +2n^2 +n−42=0 (n−2)(n+3)(n^2 +n+7)=0 ∴ n=2 is only natural root.

$${Once}\:{we}\:{found}\:{n}=\mathrm{2}\:\wedge\:{A}=\mathrm{7} \\ $$$${We}'{ve}\:{to}\:{prove}\:{that}\:{there}'{s}\:{no} \\ $$$${other}\:{natural}\:{root}\:{of}\:{f}\left({n}\right). \\ $$$${For}\:{this}\:{put}\:{A}=\mathrm{7}\:{in}\:{f}\left({n}\right)\:{and} \\ $$$${then}\:{trying}\:{to}\:{solve}\:{f}\left({n}\right)\:{whose} \\ $$$${one}\:{factor}\:{is}\:{already}\:{known}:\:{n}−\mathrm{2} \\ $$$$ \\ $$$${n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}\:−\:{A}^{\mathrm{2}} =\mathrm{0}\:\:\:\:\left({A}\in{N}\right) \\ $$$${n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}+\mathrm{7}\:−\:\mathrm{7}^{\mathrm{2}} =\mathrm{0}\:\:\:\: \\ $$$${n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}−\mathrm{42}=\mathrm{0}\:\:\:\: \\ $$$$\left({n}−\mathrm{2}\right)\left({n}+\mathrm{3}\right)\left({n}^{\mathrm{2}} +{n}+\mathrm{7}\right)=\mathrm{0} \\ $$$$\therefore\:{n}=\mathrm{2}\:{is}\:{only}\:{natural}\:{root}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com