
Question Number 124302 by Dwaipayan Shikari last updated on 02/Dec/20
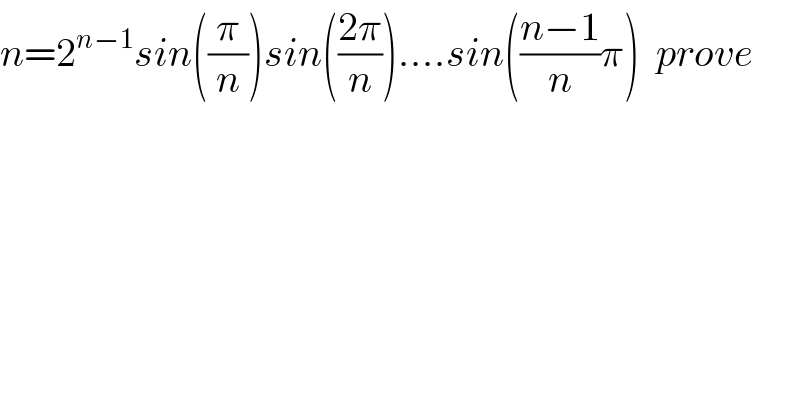
$${n}=\mathrm{2}^{{n}−\mathrm{1}} {sin}\left(\frac{\pi}{{n}}\right){sin}\left(\frac{\mathrm{2}\pi}{{n}}\right)....{sin}\left(\frac{{n}−\mathrm{1}}{{n}}\pi\right)\:\:{prove}\: \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 02/Dec/20
![solution z^n −1=0 [re^(inθ) =e^(i2kπ) ,k∈Z] [r=1, θ_k =((2kπ)/n) ,k=1,...,n−1] (z−1)(z−z_1 )(z−z_2 )...(z−z_(n−1) )=0 where z_1 ,...,z_(n−1) ∈C and (z−z_1 )...(z−z_(n−1) )=z^(n−1) +z^(n−2) +...+z+1 (∗) z=1 both sides of (∗) (1−z_1 )...(z−z_(n−1) )=(1+...+1)+1=n C=(1−e^((i2π)/n) )(1−e^((i4π)/n) )...(1−e^((i(2n−2)π)/n) ) =n ∣C∣=1⇒∣2sin^2 ((π/n))−2isin((π/n))cos((π/n))∣...∣2sin^2 ((((n−1)π)/n))−2isin((((n−1)π)/n))cos((((n−1)π)/n))∣=n ⇒ 2^(n−1) sin((π/n))sin(((2π)/n))...sin((((n−1)π)/n))=n .........✓ corallary: ∫_0 ^( (π/2)) log(sin(x))dx=−(π/2)log(2)](Q124305.png)
$${solution} \\ $$$$\:{z}^{{n}} −\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\left[{re}^{{in}\theta} ={e}^{{i}\mathrm{2}{k}\pi} \:\:,{k}\in\mathbb{Z}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{r}=\mathrm{1},\:\theta_{{k}} =\frac{\mathrm{2}{k}\pi}{{n}}\:,{k}=\mathrm{1},...,{n}−\mathrm{1}\right] \\ $$$$\:\:\left({z}−\mathrm{1}\right)\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)...\left({z}−{z}_{{n}−\mathrm{1}} \right)=\mathrm{0} \\ $$$$\:\:\:\:{where}\:\:{z}_{\mathrm{1}} ,...,{z}_{{n}−\mathrm{1}} \in\mathbb{C}\:{and} \\ $$$$\:\left({z}−{z}_{\mathrm{1}} \right)...\left({z}−{z}_{{n}−\mathrm{1}} \right)={z}^{{n}−\mathrm{1}} +{z}^{{n}−\mathrm{2}} +...+{z}+\mathrm{1}\:\left(\ast\right) \\ $$$$ \\ $$$$\:\:{z}=\mathrm{1}\:{both}\:{sides}\:{of}\:\left(\ast\right)\: \\ $$$$\left(\mathrm{1}−{z}_{\mathrm{1}} \right)...\left({z}−{z}_{{n}−\mathrm{1}} \right)=\left(\mathrm{1}+...+\mathrm{1}\right)+\mathrm{1}={n} \\ $$$${C}=\left(\mathrm{1}−{e}^{\frac{{i}\mathrm{2}\pi}{{n}}} \right)\left(\mathrm{1}−{e}^{\frac{{i}\mathrm{4}\pi}{{n}}} \right)...\left(\mathrm{1}−{e}^{\frac{{i}\left(\mathrm{2}{n}−\mathrm{2}\right)\pi}{{n}}} \:\right)\:={n} \\ $$$$\mid{C}\mid=\mathrm{1}\Rightarrow\mid\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{{n}}\right)−\mathrm{2}{isin}\left(\frac{\pi}{{n}}\right){cos}\left(\frac{\pi}{{n}}\right)\mid...\mid\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right)−\mathrm{2}{isin}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right){cos}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right)\mid={n} \\ $$$$\Rightarrow\:\mathrm{2}^{{n}−\mathrm{1}} {sin}\left(\frac{\pi}{{n}}\right){sin}\left(\frac{\mathrm{2}\pi}{{n}}\right)...{sin}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right)={n}\:\:\:\: \\ $$$$\:\:\:\:\:.........\checkmark \\ $$$$ \\ $$$$\:{corallary}:\:\:\: \\ $$$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {log}\left({sin}\left({x}\right)\right){dx}=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 02/Dec/20
$${Great}\:!\:{thanking}\:{you} \\ $$
Commented by mnjuly1970 last updated on 02/Dec/20

$${grateful}\:... \\ $$
