
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 196447 by cortano12 last updated on 25/Aug/23
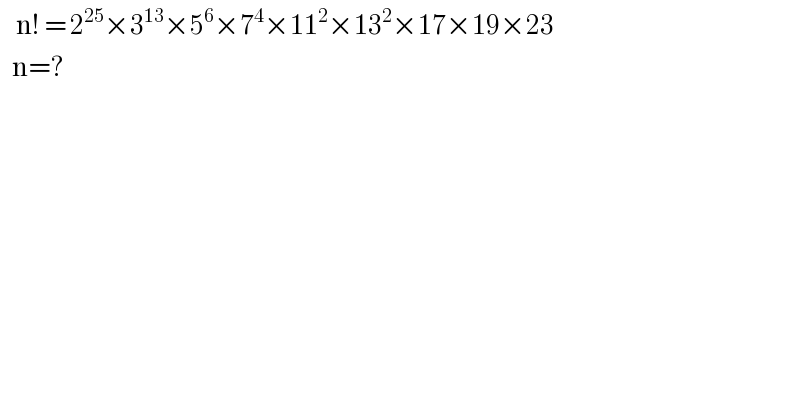
$$\:\:\:\:\mathrm{n}!\:=\:\mathrm{2}^{\mathrm{25}} ×\mathrm{3}^{\mathrm{13}} ×\mathrm{5}^{\mathrm{6}} ×\mathrm{7}^{\mathrm{4}} ×\mathrm{11}^{\mathrm{2}} ×\mathrm{13}^{\mathrm{2}} ×\mathrm{17}×\mathrm{19}×\mathrm{23} \\ $$$$\:\:\:\mathrm{n}=? \\ $$
Answered by Frix last updated on 25/Aug/23

$$\mathrm{2}\:\mathrm{6}\:\mathrm{10}\:\mathrm{14}\:\mathrm{18}\:\mathrm{22}\:\mathrm{26} \\ $$$$\mathrm{4}\:\mathrm{12}\:\mathrm{20}\:\mathrm{28} \\ $$$$\mathrm{8}\:\mathrm{24} \\ $$$$\mathrm{16} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}^{\mathrm{25}} \:\mathrm{is}\:\mathrm{included}\:\mathrm{in}\:\mathrm{28}!\:\mathrm{and}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{29} \\ $$$$\Rightarrow \\ $$$${n}=\mathrm{28} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Aug/23

$$\vee\:\cap\boldsymbol{\mathrm{i}}\subset\in! \\ $$
Answered by som(math1967) last updated on 25/Aug/23
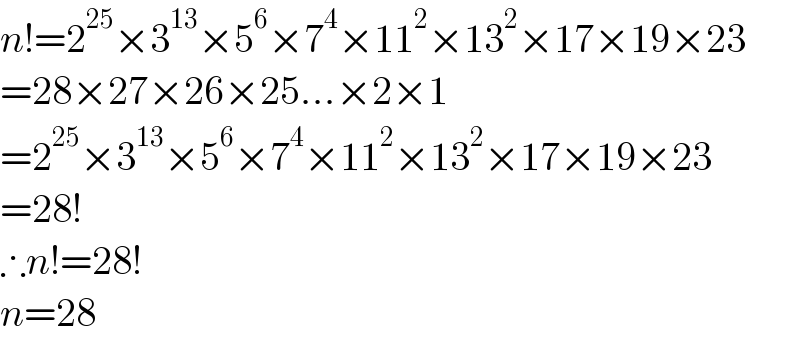
$${n}!=\mathrm{2}^{\mathrm{25}} ×\mathrm{3}^{\mathrm{13}} ×\mathrm{5}^{\mathrm{6}} ×\mathrm{7}^{\mathrm{4}} ×\mathrm{11}^{\mathrm{2}} ×\mathrm{13}^{\mathrm{2}} ×\mathrm{17}×\mathrm{19}×\mathrm{23} \\ $$$$=\mathrm{28}×\mathrm{27}×\mathrm{26}×\mathrm{25}...×\mathrm{2}×\mathrm{1} \\ $$$$=\mathrm{2}^{\mathrm{25}} ×\mathrm{3}^{\mathrm{13}} ×\mathrm{5}^{\mathrm{6}} ×\mathrm{7}^{\mathrm{4}} ×\mathrm{11}^{\mathrm{2}} ×\mathrm{13}^{\mathrm{2}} ×\mathrm{17}×\mathrm{19}×\mathrm{23} \\ $$$$=\mathrm{28}! \\ $$$$\therefore{n}!=\mathrm{28}! \\ $$$${n}=\mathrm{28} \\ $$
